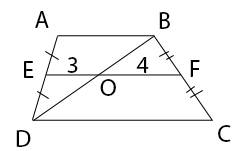
Обращаю внимание, что расстояние дано от центра до плоскости сечения, а не до хорды, являющейся основанием этого сечения.
Для ответа на вопрос задачи нам нужно знать АН -половину основания АВ треугольника АВС, который обрауется сечением, и высоту СН этого треугольника.
Высота СН состоит из 2-х отрезков - СМ и МН.
ОМ разбивает Δ СОН на два подобных треугольника СОМ и МОН( по свойству высоты прямоугольного треугольника)
Найдем по теореме Пифагора катет СМ треугольника СОМ
СМ =√(СО²-ОМ²)=√(40²-24²)=32 см
Δ СМО ~ Δ ОМН
СМ:ОМ=ОМ:МН
ОМ² =СМ*МН
576=32МН
МН=18
СН=32+18=50см - это высота равнобедренного треугольника, каким является искомой сечение.
Нужно найти АН - половину основания этого треугольника АВС
АН=√(ОА²-ОН²)
ОН=√( 50²- 40²)=30 см
АН=√(50²-30²)=40 см
S АВС=0*50=2000 см²
Площадь сечения равна 2000 см²
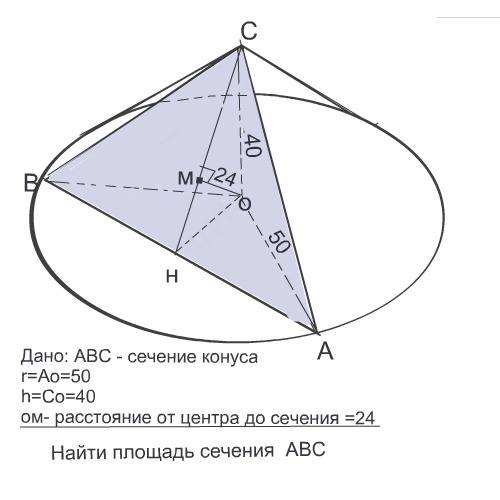
Дано: ABCD - трапеция
EF - средняя линия
EO = 3 см
OF = 4 см
Найти: AB
Решение.
1) Рассмотрим трапецию ABCD. Средняя линия EF параллельна основаниям AB и DC и делит стороны AD и BC трапеции пополам.
2) Рассмотрим треугольники EOD и ABD.
Углы EOD и ABD равны как соответственные при пересечении параллельных прямых EF и AB секущей BD.
Угол DBC общий. Следовательно, треугольник BOF подобен BDC.
3) Из подобия треугольников следует, что
AB / EO = AD / ED => AB = EO * AD / ED = EO * 2ED / ED = EO * 2 = 6 см