Лайфхак один и для маленьких, и для больших: надо находить ОД и на него сокращать. Постепенно (пошагово), или найдя НОД путем разложения на простые множители.
1) 550/418=550:2/418:2=275/209= 275:11/209/11=25/19 -постепенно делим на простые числа, пока не получим несократимую дробь
2)550:22/418:22=25/19 здесь НОД(550,418)=22=2*11
Здесь 2 и 11 -простые числа, просто подбираем из таблицы, есть куча сайтов с калькулятора ми сокращения дробей
3) 3255 /3720= 3255 : 465 / 3720 : 465 = 7/8. Здесь 465 -это НОД обоих чисел: 465=3*5*31 -простые числа
Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
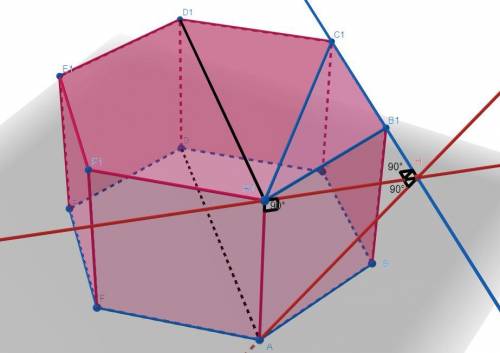
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.

A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
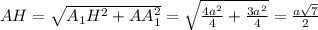
ответ: 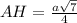
Квадрат гипотенузы равен сумме квадратов катетов
( а²=в²+с² ) .
Тогда :
1)х²= 6²+8² ;
х²=36+64 ;
х²=100 ;
х=√100 ;
х=10 - гипотенуза .
ответ : 10 .
2)х²=4²+7² ;
х²=16+49 ;
х²=65 ;
х = √65 .
ответ : √65 .