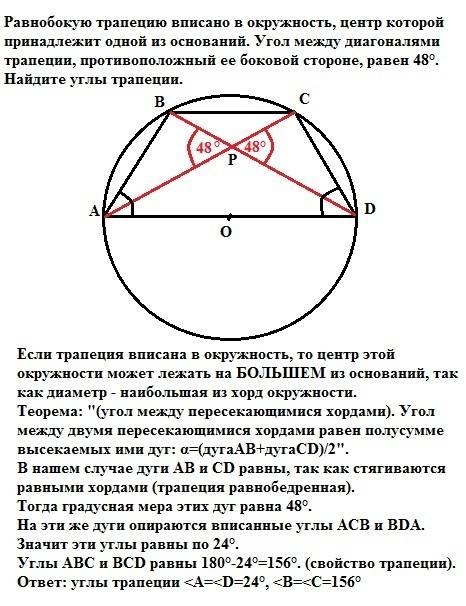
118°, 118°, 62°, 62°
Объяснение:
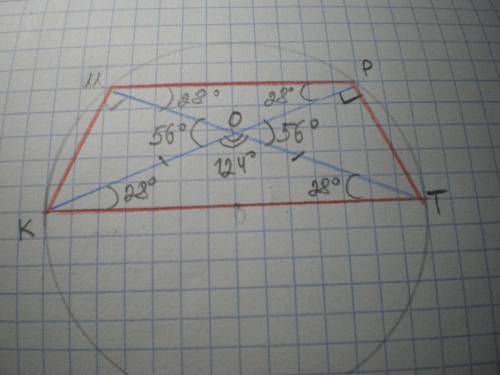
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
ВD=6•2=12 см
По условию BD:DC=3:2, значит, длина одной части равна этого отношения 12:3= 4 см.
DC=4•2=8см ⇒
ВС=12+8=20 (см)
∠BDC– развернутый и равен 180°
∠АDC= ∠BDC-∠ADC=180°-100°=80°
Средняя линия треугольника параллельна его основанию. AD - секущая при параллельных KF и АD.⇒
∠АFK=∠ADB=80°как соответственные.
2. АВ=8, если АВ больше АС в 2 раза, то угол СВА=30
В прямоугольном треугольнике катет напротив угла в 30 градусов равен половине гипотенузы. СМ - медиана,
значит ВМ=Ма=4
То СМА получается равнобедренный, значит МСА=АМС=180-60/2=60
угол ВСМ = 90-МСА = 30 3. находим полусумму оснований (8+12)/2=10
находим боковую сторону (12-8)/2cosa=2/cosP=4/cosa+20
находим высоту h=2tga
S=20tga
4. В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см.
5. из теоремы Пифагора находим АВ=корень из(АD^2-BD^2) Дальше площадь треугольника АВD=АВхВD/2(он прямоугольный).Следующий этап находим высоту этого же треуг-ка,опущенную на АD-она равна DЕ. Делим площадь этого треугольника на половину основания (АD) Теперь в прямоуголном треугольнике нам известны гипотенуза ВД и катетDЕ Опять применим теорему Пифагора ВЕ=корень из(ВD^2-DE^2)