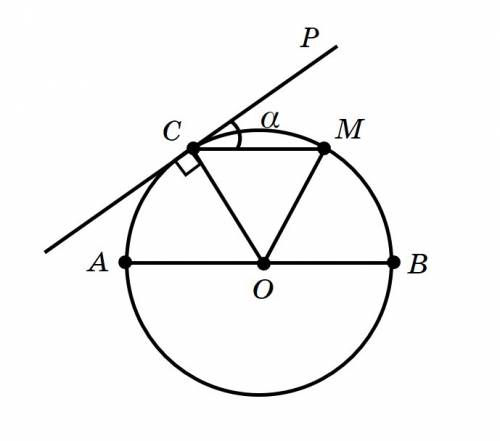
Геометрическим местом точек пространства равно удаленных от двух данных точек и , является плоскость , перпендикулярная к отрезку прямой, соединяющему эти точки, и проходящая через его середину.
Находим координаты точки А как середины отрезка ОВ: А(1; 1,5; 2,5).
Направляющий вектор прямой ОВ (координаты О равны нулям) равен значениям координат точки В: ОВ(2; 3; 5).
Уравнение плоскости, которая проходит через точку (x0,y0,z0) перпендикулярно вектору (A,B,C) имеет вид
A(x−x0)+B(y−y0)+C(z−z0)=0.
2(x−1)+3(y−1,5)+5(z−2,5)=0.
ответ: это плоскость с уравнением 2x + 3y+ 5z - 19 = 0.
Пользуясь рисунком, (см. вложение) и зная, что 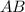 — диаметр окружности,
— диаметр окружности, 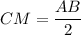 — хорда окружности, определим
— хорда окружности, определим 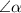 .
.
В окружности половиной диаметра являются радиусы, значит, эти радиусы будут равны и хорде: 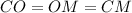
В образовавшемся треугольнике 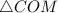 получается, что все три стороны по длине равны, следовательно, этот треугольник является равносторонним, у которого все углы равны по
получается, что все три стороны по длине равны, следовательно, этот треугольник является равносторонним, у которого все углы равны по 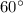 .
.
Как известно, точка касания касательной к окружности и радиуса окружности пересекаются под прямым углом (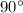 ).
).
Отсюда следует, чтобы узнать 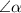 , нужно найти разность развёрнутого угла (
, нужно найти разность развёрнутого угла (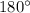 ) от суммы других известных углов:
) от суммы других известных углов:
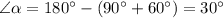
ответ: 30°