асательная прямая t к окружности c пересекает окружность в единственной точке t. для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. это свойство касательной прямой сохраняется при многих преобразованиях[en], таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. и обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
по теореме о степени точкипроизведение длин pm•pn для любого луча pmn равно квадрату pt, длине отрезка от точки p до точки касания (отрезок показан красным цветом).никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. в то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку p с центром окружности o (см. рисунок справа). в этом случае отрезки от точки p до двух точек касания имеют одинаковую длину. по теореме о степени точки квадрат длины отрезка до точки касания равен степени точки p относительно окружности c. эта степень равна произведению расстояний от точки p до двух точек пересечения окружности любой секущей линией, проходящей через p.
угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.касательная прямая t и точка касания t свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. такая же взаимосвязь существует между точкой p вне окружности и секущей линией, соединяющей две точки касания.
если точка p лежит вне окружности с центром o, и если касательные прямые из p касаются окружности в точках t и s, то углы ∠tps и ∠tos в сумме 180°.
если хорда tm проведена из точки касания t прямой p t и ∠ptm ≤ 90°, то ∠ptm = (1/2)∠mot.
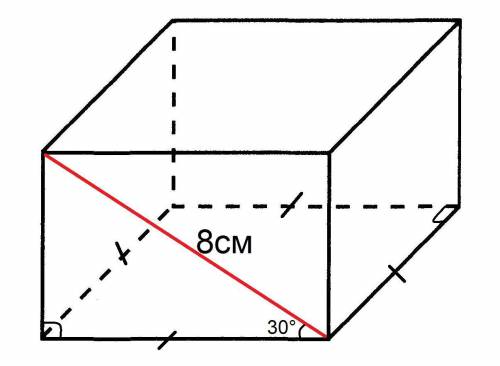
Рассмотрим один из двух треугольников, полученных при проведении диагонали в боковой грани параллелепипеда:
Треугольник прямоугольный т.к. параллелепипед прямой, по этой же причине один из острых углов равен 30°; гипотенуза (диагональ боковой грани) равна 8см; катет лежащий напротив угла в 30° (боковое ребро) равен половине гипотенузы: 8см:2 = 4см; другой катет (сторона основания), по теореме Пифагора, равен √(8²-4²) = √(64-16) = √48 см.
Объём параллелепипеда можно найти через его высоту (в нашем случаи это и боковое ребро) и площадь основания. В основании лежит квадрат, поэтому его площадь равна (√48 см)² = 48 см².
Тогда объём равен 4см · 48см² = 192 см³
ответ: 192см³.
Дано: АВСД – параллелограмм, АЕ – биссектриса, угол ВАЕ=21 °.
Найти угол А.
Биссектриса ∠ВАД делит его пополам.
Угол А=2*21=42 ° (по свойству биссектрисы).
ответ: 42 градуса