1) Даны точки М(3; 5) и N(-6; -1).
Угловой коэффициент к прямой, проходящей через эти точки равен:
к = Δу/Δх = (-1-5)/(-6-3) = -6/-9 = 2/3.
Уравнение прямой будет у = (2/3)х + в.
Для определения величины в подставим в это уравнение координаты одной из точек, возьмём А.
5 = (2/3)*3 + в, отсюда в = 5 - 2 = 3.
ответ: уравнение у = (2/3)х + 3.
В общем виде 2х - 3у + 9 = 0 (после приведения к общему знаменателю).
2) Пусть точка N, лежащая на оси абсцисс
и равноудаленная от точек Р(-1; 3) и К(0; 2), имеет координаты N(x; 0).
Используем равенство расстояний точки N от P и K.
NP² = (-1 - x)² + (3 - 0)² = 1 + 2x + x² + 9 = 10 + 2x + x².
NK² = (0 - x)² + (2 - 0)² = x² + 4.
Приравняем 10 + 2x + x² = x² + 4,
2x = 4 - 10
x = -6/2 = -3.
ответ: точка N(-3; 0).
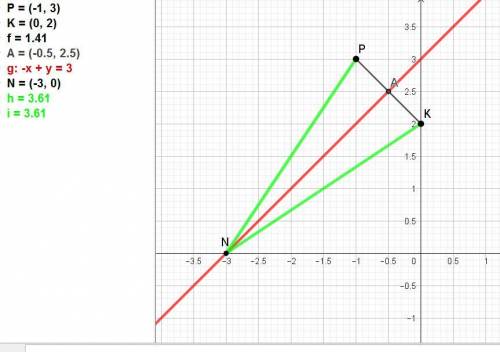
К этому решению во вложении дан поясняющий рисунок.
Из него видно, что есть второй решения задания с использованием срединного перпендикуляра к отрезку АВ.
Приложим треугольник ABC (либо симметричный ему) к треугольнику A1B1C1 так, чтобы вершина А совместилась с вершиной A1, вершина В — с вершиной В1, а вершины С и С1, оказались по разные стороны от прямой А1В1. Рассмотрим 3 случая:
1) Луч С1С проходит внутри угла А1С1В1. Так как по условию теоремы стороны АС и A1C1, ВС и В1С1 равны, то треугольники A1C1C и В1С1С — равнобедренные. По теореме о свойстве углов равнобедренного треугольника ∠1 = ∠2, ∠3 = ∠4, поэтому ∠ACB=∠A1C1B1.
2) Луч С1С совпадает с одной из сторон этого угла. A лежит на CC1. AC=A1C1, BC=B1C1, C1BC – равнобедренный, ∠ACB=∠A1C1B1.
3) Луч C1C проходит вне угла А1С1В1. AC=A1C1, BC=B1C1, значит, ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A1C1B1.
Итак, AC=A1C1, BC=B1C1, ∠C=∠C1. Следовательно, треугольники ABC и A1B1C1 равны по
первому признаку равенства треугольников.