Sполн = 16(12+√3)/3 см².
Объяснение:
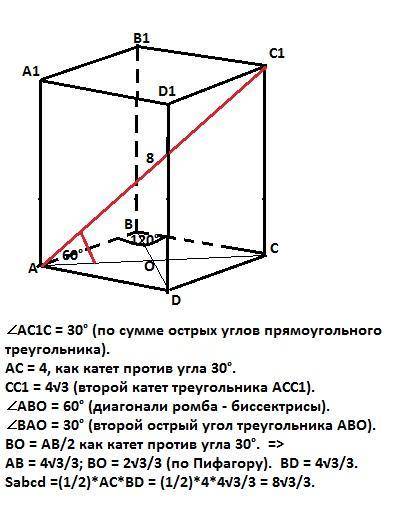
∠АС1С = 30° (по сумме острых углов прямоугольного треугольника).
АС = 4см (катет против угла 30°).
СС1 = 4√3см (второй катет треугольника АС1С).
∠АВО = 60° (диагонали ромба - биссектрисы).
∠АВО = 30° ( второй острый угол - диагонали ромба взаимно перпендикулярны).
ВО = АВ/2 как катет против угла 30°.
АВ = 4√3/3 см; ВО = 2√3/3см (по Пифагору). BD = 4√3/3см.
Sabcd = (1/2)·AC·BD = (1/2)·4·4√3/3 = 8√3/3см².
Sграни = АВ·СС1 = 4√3/3·4√3 = 16см².
S = 2·Sabcd+4·Sграни = 16√3/3 +4·16 = 16(12+√3)/3 см².
2.Высота делит этот треугольник на два, один из которых равнобедренный прямоугольный. (Угол 45 градусов по условию, второй после построения высоты)
Катеты в нем равны.
Обозначим каждый х,
-один из катетов часть основания, второй катет - высота.
Квадрат гипотенузы равен сумме квадратов двух катетов:
2х²=49*2
х²=49
х=7 см
Высота равна 7, основание треугольника 10.
S=1/2h*a
S=7*10:2=35 cм
3.В трапеции АВСД АВ=СД=10 см, АС=17 см, АД-ВС=12 см.
Проведём СН⊥АД.
В равнобедренной трапеции ДН=(АД-ВС)2=12/2=6 см.
Тр-ник CДН - египетский т.к. отношение гипотенузы и катета равны 5:3 (СД/ДН=10/6=5/3), значит СН=4·2=8 см.
В прямоугольном тр-ке АСН АН²=АС²-СН²=17²-8²=225,
АН=15 см,
АД=АН+ДН=15+6=21 см.
АД-ВС=12 ⇒ ВС=АД-12=21-12=9 см.
S=CН·(АД+ВС)/2=8(21+9)/2=120 см² - это ответ.
3x+30=180
3x=150
x=50