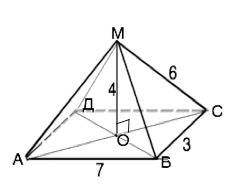
Обозначим пирамиду МАВСД,
АС - большая диагональ, АВ=СД=7, ВС=АВ=3, высота МО=4
Пусть большим ребром будет МС. Тогда его проекция на основание - ОС больше проекции ребра МВ, и . АС - большая диагональ основания пирамиды.
МО⊥АС, АО=ОС, ∆ МОС - прямоугольный.
По т.Пифагора ОС=√(MC²-MO²)=√20=2√5
Отсюда АС=4√5 - это длина большей диагонали.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
АС²+ВД²=2(АВ²+ВС*)
80+ВД²=116
ВД²=36
ВД=6 это длина меньшей диагонали основания.
Диагонали основания 4√5 и 6 (ед. длины).
Проекция апофемы A на основание правильной треугольной пирамиды равна 1/3 высоты h основания.
Или (1/3)h = (1/3)*(a*cos 30°) = (1/3)*6*(√3/2) = √3 см .
Тогда апофема А = ((1/3)h)/(cos 45°) = √3/(√2/2) = √6 см.
Площадь основания So = a²√3/4 = 36√3/4 = 9√3 см².Периметр основания Р =3а = 3*6 = 18 см.
Площадь боковой поверхности Sбок = (1/2)PA = (1/2)*18*√6 = 9√6 см².Искомая площадь полной поверхности пирамиды равна:Sп = Sо + Sбок = 9√3 + 9√6 = 9(√3 + √6) = 9√3(1 + √2) ≈ 37,63386 см².