остроугольный и равнобедренный.
Объяснение:
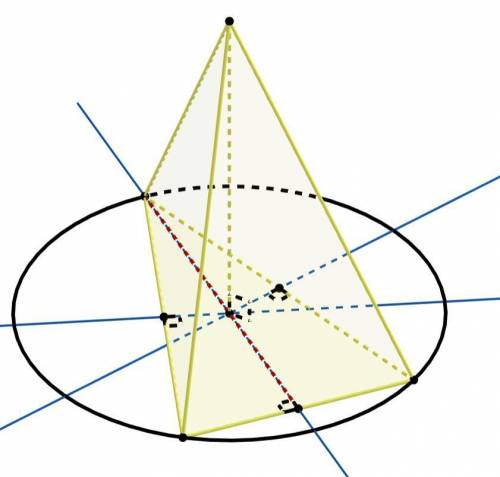
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
По условиям задачи треугольник ABC равнобедренный, значит его биссектриса так же является и медианой и высотой. Раз она медиана, то она делит основание AC на две равные части AK и CK.
Треугольники ABK и CBK равны по двум сторонам и углу между ними - AK=CK, BK у них одна и та же, а углы AKB и CKB тоже равны между собой(они оба равны 90° потому что биссектриса в равнобедренном треугольнике является также и высотой - перпендикуляром из вершины к основанию). Следовательно и периметры этих треугольников равны - 12 см
Сумма периметров этих треугольников ABK+CBK= AB+BK+AK+BC+BK+CK =24 см, периметр ABC= AB+BC+AC =20 см, следовательно можно наложить их друг на друга и сократить совпадающие участки - AB, DC и AC=AK+CK.
(AB+BK+AK+BC+BK+CK)-(AB+BC+AC) = 24-20
2BK = 4
BK = 2