а)уравнение стороны AB = -8х+4у+84=0, BC=2х+14у-6=0, AC=-10х-10у-30=0. Можно представить эти уравнения с угловым коэффициентом в виде y = kx + a. Для этого перенесем все значения кроме y в правую часть, например: 4y = 8x - 84. Затем разделим правую часть на коэффициент 4. Получим: y = 2x - 21. б)уравнение высоты CH можно составить, зная координату точки Н(8;-5) СН = 6х+12у+12=0. в)уравнение медианы AM можно составить, зная координату точки М(3;0) АМ = -9х-3у+27=0. г)точку N пересечения медианы AM и высоты CH: так как заданный треугольник равнобедренный (а=в=14,1421), то высота на сторону АВ является и медианой. Поэтому точка N - центр тяжести треугольника. N(4;-3). д)уравнение прямой,проходящей через вершину C параллельно стороне AB = у-2х-9=0 или у = 2х+9. е)расстояние от точки C до прямой AB - это высота СН = 13,4164.
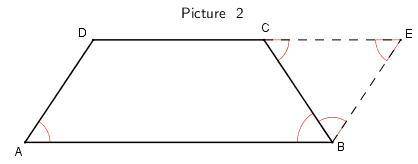
Предоставлю точно также два решения только другой метод(более рационален). Из вершины D продлим сторону до пересечения на продлении стороны BC, так что AB ║ DE, т.е. ABED — параллелограмм.
∠A = ∠E = 60° (противоположные углы у параллелограмма равны)
Так как AB = CD ⇒ ED = CD ⇒ ∠ECD = ∠CED = ∠CDE = 60°, т.е. треугольник CDE — равносторонний ⇒ CD = CE = ED = 32
Тогда AD = BC + CE = 20 + 32 = 52
P = 20 + 32 + 32 + 52 = 136
Рисунок 2.
Аналогично решению из рисунка 1, достроим до параллелограмма ADEB, AD ║ EB, мы имеем что ΔCEB - равносторонний, т.е. CE = CB = EB = 20, тогда CD = AB - CE = 32 - 20 = 12.
P = 12 + 20 + 20 + 32 = 84

11+19=30
30/2=15