Вариант решения.
ответ: 36 ед. объёма
Объяснение:
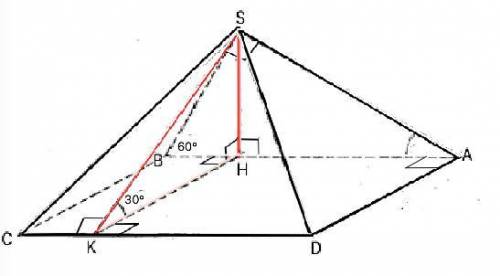
Углы между плоскостями боковых граней и плоскостью основания - двугранные. Их величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём. Обозначим пирамиду SABCD . Пусть перпендикулярна плоскости АВСD грань ЅАВ ⇒ её высота ЅН перпендикулярна любой прямой в этой плоскости.
Проведём НК║ВС. Т.к. АВСD прямоугольник, НК⊥СD, и наклонная ЅК⊥CD по т.о 3-х перпендикулярах⇒ ∠ЅКН =30°.
В прямоугольном ⊿ ЅНК с острым углом 30° гипотенуза ЅК=2 катета ЅН, который противолежит углу 30° (свойство) ⇒ 2ЅН+ЅН=9, откуда ЅН=3.
В ⊿ ВЅН угол В=60° ⇒ ВЅ=ЅН:sin60°=2√3
В ⊿ ВЅА гипотенуза АB=ЅВ•cos60°=4√3
В ⊿ ЅКН угол ЅКН=30° ⇒ KH=SH•ctg30°=3√3
Формула объёма пирамиды V=S•h:3, где Ѕ - площадь основания пирамиды, h- её высота. АD=KH=3√3
V=AB•AD•SH/3=4√3•3√3•3/3=36 (ед. объёма).
O₁O₂=16 см
O₂A>O₁A
1) Окружности касаются внешним образом.
В этом случае отрезок, соединяющий центры, является суммой радиусов.
O₁A+O₂A=O₁O₂
O₁A=x, O₂A=3x
x+3x=16 <=> 4x=16 <=> x=4 (см)
O₁A=4 см
O₂A=3*4 =12 см
2) Окружности касаются внутренним образом.
В этом случае отрезок, соединяющий центры, является разностью радиусов.
O₂A-O₁A=O₁O₂
O₁A=x, O₂A=3x
3x-x=16 <=> 2x=16 <=> x=8 (см)
O₁A=8 см
O₂A=8*3 =24 см