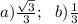
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
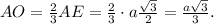
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
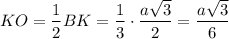
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
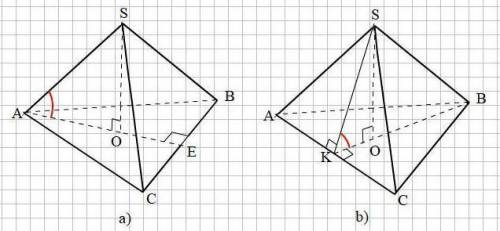
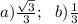
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
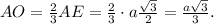
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
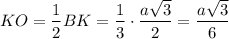
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.

1) Зная, что R=2а найдем сторону основания по формуле R=AВ√3/3, отсюда АВ=3R/√3=3*2a/√3=6a/√3.
Рассмотрим прямоугольный треугольник СМВ (угол М=90 градусов, МВ=АВ/2=3а√3, ВС=6a/√3). По теореме Пифагора МС=√(ВС^2-MB^2)= √(36а^2/3-9a^2/3)= √(12a^2-3a^2)= √9a^2=3a. Медиана разбивается точкой О на отрезки пропорциональные 2:1 от вершины. Таким образом отрезок СО=2а, Ом=а.
Рассмотрим прямоугольный треугольник МОК (угол О=90 градусов, МО=а, КО=а√3). По теореме Пифагора найдем МК, которая является апофемой. МК=√(МО^2+KO^2)= √(a^2+3a^2)= √4a^2=2a/
2) Тангенс угла КМО=КО/МО=а√3/а=√3, значит угол КМО=60 градусов (угол между боковой гранью и основанием) .
3) Площадь боковой поверхности = ½ * периметр основания * апофему=1/2 * 3*6а/√3 * 2а=18а^2/√3=6√3а^2.