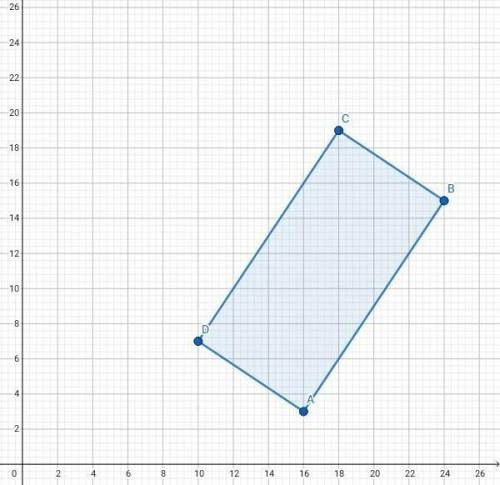
Модуль вектора |a|= 13 ,|b| = 19,|a +b | = 24. Найдите | a-b |.
Объяснение:
1) Рассмотрим ΔАВС, вектор а лежит на стороне АВ, вектор b лежит на стороне АD . Разность векторов а-b=DВ ( вектор) Уточняю длина ( или модуль) вектора равна длине отрезка на котором он лежит. Значит нужно найти отрезок DВ и АВ=13,АD=19 .
2) Достроим ΔАВD до параллелограмма , тогда сумма векторов а+b=АВ+АD=( по правилу параллелограмма ) = вектору АС. Тогда |AC|=|a+b|=24. Значит длина отрезка АС=24. По свойству диагоналей параллелограмма АО=12( О-точка пересечения диагоналей).
3) По свойству диагоналей параллелограмма: "сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон " имеем: AC²+BD²=2(AB²+AD²)
24²+BD²=2(13²+19²), BD=√(2*(169+361)-576)=√484=22.
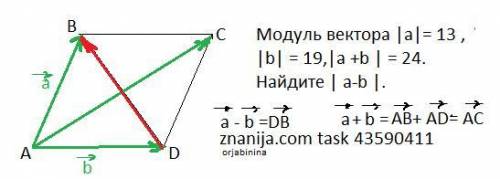
1. Вспомним признак прямоугольника: если в четырёхугольнике три угла равны по 90°, то этот четырёхугольник - прямоугольник. Рассмотрим и проверим этот признак в данной задаче:
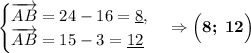
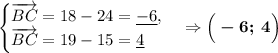
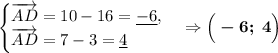
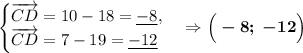
Вспомним свойство о скалярном произведении векторов: если произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны. Найдём такие пары векторов:
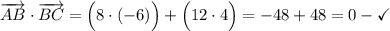
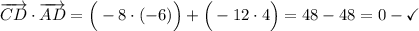
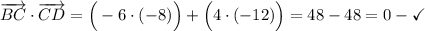
Теперь мы можем утверждать, что фигура "ABCD" - прямоугольник, т.к. углы "B", "C" и "D" составляют по 90° каждый.
Что и требовалось доказать.
2. Площадь прямоугольника - произведение его длины и ширины. Поэтому сначала нужно найти, чему равна длина и ширина.
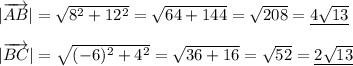
Теперь, когда нам известна и длина, и ширина, найдём площадь прямоугольника:
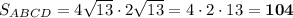 см².
см².
ответ: 104 см².