В прямоугольный ΔАВС, ∠С=90 вписан круг .Биссектриса ∠А делит катет в отношении CD:DB=3:5. Найдите площадь круга
Решение Площадь круга S= πr² .Радиус вписанной окружности найдем из формулы S=1/2*P*r .
1) Тк " биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника" , то CD:СА=ВD:АВ или 3:СА=5:АВ ⇒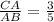
, а это по определению sinB .
2) По основному тригонометрическому тождеству
sin²B+cos²B=1 получаем cosB=√(1-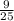
)=
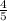
3) cosB=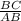 
или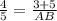 
⇒ AB=10.
По т Пифагора АС=√(АВ²-ВС²)=√(100-64)=6
4) S=1/2*P*r
1/2*BC*AC=1/2*(AB+BC+AC)*r
1/2*8*6=1/2*24*r ⇒ r=2 ед
S(круга)=π*2²=4π (ед²)
Дано: Треугольник АВС. АВ=ВСб М∈BD, K∈AC. MK║AB. <ABC=126°,<BAC=27°.
Найти <MKD, <KMD и <MDK.
Решение.
Треугольник АВС равнобедренный, следовательно BD - биссектриса, высота и медиана треугольника. <BAC=<BCA=27°, Значит
<ABD = (1/2)*(<ABC) = 126/2 = 63°. <BDA=<MDK = 90°.
MK параллельна АВ, значит <MKD=<BAC=27°, а <KMD=<ABD=63°, как соответственные углы при параллельных прямых АВ и МК и секущих AD и BD соответственно.
ответ: <MKD=27°, <KMD=63°, <MDK=90°.
S=a^3/4R=a^3/4(a√3/2)
25√3=a^3/4(a√3/2)
a=(5√6)/2
P=3*(5√6)/2)=(15√6)/2)