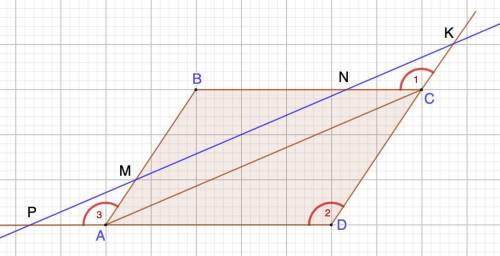
Объяснение:
Дано: ABCD - параллелограмм;
РК║АС
Доказать: РМ=NK
Доказательство:
1) Рассмотрим АМКС.
АМ║СК (ABCD - параллелограмм)
МК║АС (условие)
⇒ АМКС - параллелограмм (по определению)
⇒ АМ=СК (свойство параллелограмма)
2) Рассмотрим PNCA.
АP║СN (ABCD - параллелограмм)
PN║AC (условие)
⇒ PNCA- параллелограмм (по определению)
⇒ АP=СN (свойство параллелограмма)
3) Рассмотрим ΔРМА и ΔNKC
АМ=СК (п.1)
АP=СN (п.2)
∠1=∠2 - соответственные при BC║AD и секущей DK
∠3=∠2 - соответственные при AB║DK и секущей DP
⇒ ∠1=∠3
⇒ ΔРМА = ΔNKC (по двум сторонам и углу между ними)
⇒ PM=NK
1. находим третий угол трегольника - 180-96=84 грудуса (т.к сумма углов треугольника равна 180 граусов). теперь находим смежный ему угол - 180-84=96 грудусов (т.к. сумма смежных углов равна 180 градусам. Или можно проще: такой смежный угол называется внешним и внешний угол равен сумме двух угол в не смежных с ним то есть 96 градусов.
2.т.к. катет равен половине гипотенузы то он лежит напротив угла в 30 градусов, то есть угол ACB=30 градусов. найдем угол ABC. 90-30=60 градусов (т.к сумма острых уголв прямоугольного треугольника равна 90 градусов).