А₁В₁С₁Д₁ -ромб, площадь которого равна А₁С₁*В₁Д₁/2=6*12/2=36/cм²/. Зная половины диагоналей 6/2 и 12/2, можно найти сторону, т.к. диагонали пересекаются под прямым углом. значит. сторона равна √(3²+6²)=
√(9+36)=3√5, ∠СВ₁С₁=30°. т.к. В₁С₁- проекция В₁С на плоскость основания. Тогда высота призмы СС₁=В₁С₁**tg30°=
3√5*(1/√3)=√15
Объем равен произведению площади на высоту. т.е. 36*√15=/см³/
Площадь полной поверхности состоит из двух площадей основания, т.е. 2*36=72, и боковой поверхности 4*В₁С₁*СС₁=4*(3√5)*(√15)=60√3
=4*3*3*5√3=90√3
площадь полной поверхности равна (72+60√3) см²
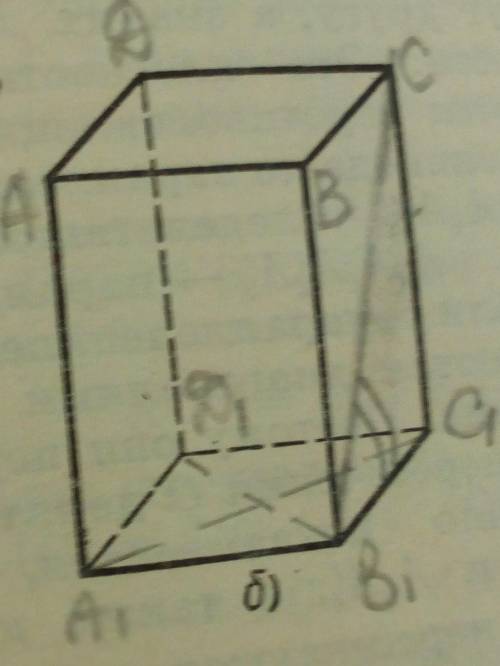
Теорема
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство. Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, AB = A1B1, AC = A1C1.
Пусть есть треугольник A1B2C2 – треугольник равный треугольнику ABC, с вершиной B2, лежащей на луче A1B1, и вершиной С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1.
Так как A1B1=A1B2, то вершины B1 и B2 совпадают.
Так как ∠ B1A1C1 = ∠ B2A1C2, то луч A1C1 совпадает с лучом A1C2.
Так как A1C1 = A1C2, то точка С1 совпадает с точкой С2. Следовательно, треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.