1. тупоугольный.
2. остроугольный.
3. прямоугольный.
Объяснение:Если 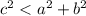 (где c - большая сторона, a, b - остальные стороны), значит данный треугольник - остроугольный.
(где c - большая сторона, a, b - остальные стороны), значит данный треугольник - остроугольный.
Если 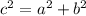 (где c - большая сторона, a, b - остальные стороны), значит данный треугольник - прямоугольный.
(где c - большая сторона, a, b - остальные стороны), значит данный треугольник - прямоугольный.
Если 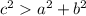 (где c - большая сторона, a, b - остальные стороны), значит данный треугольник - тупоугольный.
(где c - большая сторона, a, b - остальные стороны), значит данный треугольник - тупоугольный.
1. 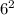 и
и 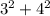
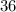 и
и 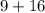
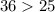
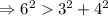 ⇒ данный треугольник - тупоугольный.
⇒ данный треугольник - тупоугольный.
2. 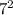 и
и 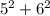
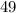 и
и 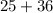
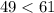
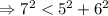 ⇒ данный треугольник - остроугольный.
⇒ данный треугольник - остроугольный.
3. 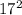 и
и 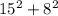
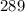 и
и 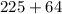
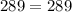
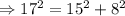 ⇒ данный треугольник - прямоугольный.
⇒ данный треугольник - прямоугольный.
Рассмотрим равнобедренный треугольник ABC с боковыми сторонами AB = BC и основанием AC.
Опустим из вершины B высоту BH на основание AC.
Рассмотрим треугольники ABH и BCH.
Так как BH - высота, то углы BHA = BHC = 90°, т.е. треугольники ABH и BCH - прямоугольные.
Заметим, что AB = BC, т.е. гипотенузы треугольников ABH и BCH равны и у них общий катет BH.
Следовательно, треугольники ABH и BCH конгруэнтны по гипотенузе и катету.
Отсюда вытекает, что AH = CH, а это означает, что BH является медианой.
Также из равенства треугольников ABH и BCH имеем, что углы ABH = CBH.
Следовательно, BH является биссектрисой угла ABC.
S1=pi*a^2
S2=pi*b^2
Гипотенуза наибольшая, тогда c=√(a^2+b^2) , c - гипотенуза
S3=4*pi*(c/2)^2=4*pi*(a^2+b^2)/4 = 4*pi*(S1+S2)/(4pi) = S1+S2