Объяснение:Имеется четыре вершины A, B, C и D, значит фигура на рисунке представляет собой четырёхугольник. Известно, что два угла четырёх угольника ∠BAD=∠BCD=90°, по обозначению углов уже понятно, что это противоположные углы и, значит, наша фигура прямоугольник. Но даны ещё два угла, которые дополняют друг друга ∠ADB=15° и ∠BDC=75°. Сумма этих углов равна 90°. То есть имеем четырёхугольник у которого известно, что три угла равны 90°, значит это прямоугольник, а у прямоугольника все стороны параллельны, т.е. AD║BC.
треугольник, а треугольник - описанным около этой окружности.
Теорема. В любой треугольник можно вписать окружность и при этом только одну.
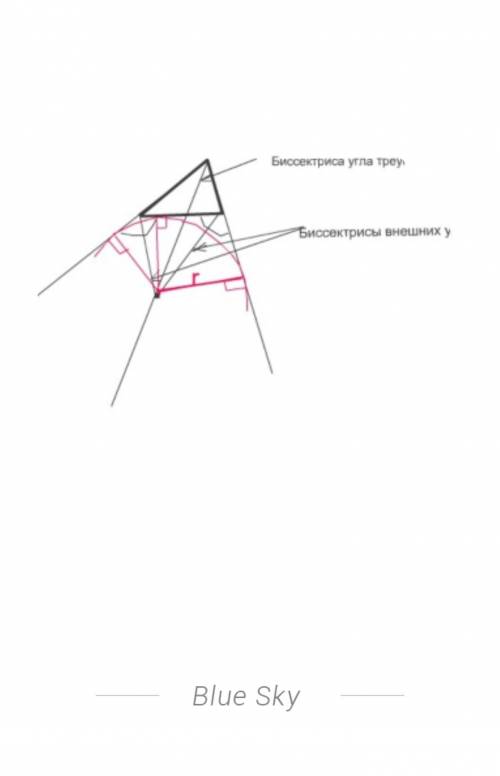
Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник - вписанным в эту окружность.
Теорема. Около любого треугольника можно описать окружность и при этом только одну.
Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.