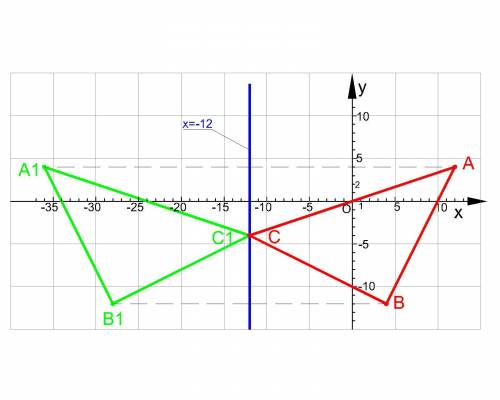
Объяснение:
1. Выполняем построение треугольника АВС.
2. Строим график прямой х = -12 . Это вертикальная прямая проходящая через точку (-12; 0)
3. Выполняем построение симметричной фигуры:
от т. А проводим перпендикуляр к прямой х = -12. Откладываем перпендикуляр такой же длины в противоположною сторону от х = -12.
То же самое выполняем для т. В. Т. С совпадает с точкой С1, т.к. абсцисса т. С = -12 и лежит на прямой х = -12.
Координаты ΔA1B1C1 можно определить графически:
А1(-36;4) , В1(-28; -12) , С1(-12; -4).
Также абсциссы можем определить математически:
х1 = -12 - (12+х) = -24-х.
Здесь -12 - это сдвиг координат влево на 12 единиц, (12+х) расстояние между осью симметрии и точками исходного треугольника.
Ординаты остаются неизменными, т.к. ось симметрии - вертикальная.
Отличающаяся сторона это основание. Т. к. остальные две должны быть равны по условию.
Тут два решения:
1. Если основание АС больше на 13 см:
АС = АВ+13
Р = АВ+ВС+АВ+13=50
т. к. АВ=ВС, то:
P= 3*АВ+13=50
3*АВ = 37
АВ = 37/3, т. е. АВ = ВС = 37/3, АС = (37/3 + 13). Проверка: (37/3 )*3+13 =50
2. Если основание АС меньше на 13 см:
АС = АВ-13
Р=АВ+ВС+АВ-13 = 50
3*АВ-13=50
3*АВ=63
АВ=21
АВ=ВС=21, АС = 21-13=8. Проверка: 21+21+8=50