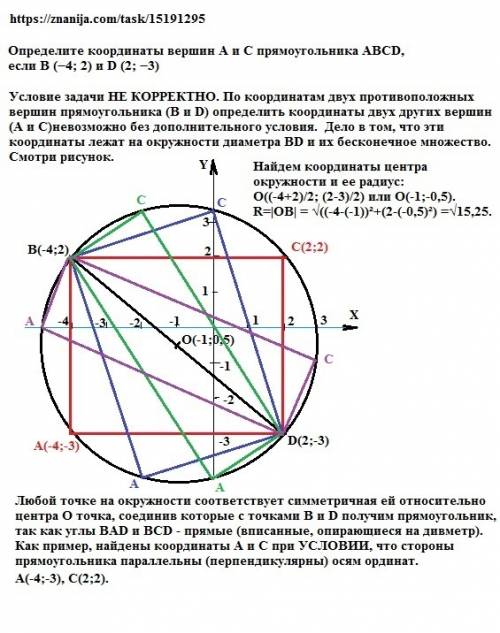
Условие задачи НЕ КОРРЕКТНО. По координатам двух противоположных вершин прямоугольника (B и D) определить координаты двух других вершин (А и С) невозможно без дополнительного условия. Дело в том, что вершины прямоугольника лежат на окружности диаметра BD и их бесконечное множество.
Смотри рисунок.
Любой точке на окружности соответствует симметричная ей относительно центра О точка, соединив которые с точками В и D получим прямоугольник, так как углы ВАD и ВСD - прямые (вписанные, опирающиеся на дивметр).
Найдем координаты центра окружности, описанной около данного прямоугольника и ее радиус:
О((-4+2)/2; (2-3)/2) или О(-1;-0,5).
R=|ОВ| = √((-4-(-1))²+(2-(-0,5)²) =√15,25. Тогда уравнение окружности (x+1)² + (y+0,5)² =15,25.
ЛЮБАЯ точка на этой окружности - вершина А, симметричная ей относительно центра О точка - вершина С.
Найдем координаты вершин А и С ПРИ УСЛОВИИ, что стороны прямоугольника параллельны осям ординат.
В уравнение окружности подставим координату Х=-4 и найдем для нее соответствующую координату Y: (-3)² + (y+0,5)² =15,25. => Y² + Y -6 = 0. => Y1=3, Y2=-2. Точно так же для точек с координатой Х=2. Y1=2 и Y2=-3. Тогда имеем: А(-4;-3) и С(2;2).
если опустить высоты из концов вехнего основания на нижнее и обозначить отсекаемые куски нижного отснования (от конца основания до ближайшего основания высоты) за x и y, то есть 2 уравнения.
x+y = 18-10 = 8;
17^2 - y^2 = 15^2 - x^2;
Я намеренно не буду решать это очень простую систему, а просто замечу, что 8, 15 и 17 - пифагоровы числа, то есть фигура с такими сторонами - прямоугольный треугольник. Поэтому x = 0 (ну решите системку сами, увидите:)). Итак, высота равна 15 :)));
Осталось понять, что проведенная через точку пересячения диагоналей высота делится точкой пересечения в отношении 18/10, то есть 9/5 (как основания, следует из подобия треугольников, образованных диагоналями и основаниями), поэтому длинна искомого отрезка равна
15*9/(9+5) = ну очень сложный ответ 135/14
второй 15*5/14 =75/14
Странно, кривой какой-то ответ, хотя 135+75=210, как и должно быть