S полной поверхности параллелепипеда = 2 S основания + 4 S боковой грани
S основания = S ромба =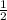
* на произведение диагоналей, одна диагональ = стороне. образовывает треугольник с углами 60 град. (формула для решения)
это равносторонний треугольник
2 диагональ из равностороннего треугольника со стороной a, и высотой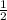 a и углом в вершине 120 град. В нем: прямоугольный треугольник с сторонами 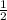*a (половина 1 диагонали), гипотенуза = a.
По т.пифагора: (корень из 3)*a/2
2 диагональ (равна корень из 3)*a
площадь основания = (корень из 3)*a*a/2.
найдем высоту. 45 град. угол между диагональю параллелепипеда и 2 диагональю ромба.
в треугольнике, образованном диагональю параллелепипеда диагональю ромба и боковой стороной параллелепипед один угол 45 град, второй = 90 град, то третий будет 180 - 45 - 90.
данный треугольник - равносторонний и высота равна диагонали ромба т.е. (корень из 3)*a. (в следствии)
Следовательно площадь боковой грани = a*(корень из 3)*a
Итого П.П.П. = 2*(корень из 3)*a*a/2 + 4*a*(корень из 3)*a = 5*(корень из 3)*(a в квадрате) (формулой)
дано: решение
c = 17 (см) p = a + b + c
a = x пусть катет a = x, тогда катет b = x - 7
b = x - 7 так как треугольник прямоугольный, то
x мы найдем по теореме пифагора:
p - ? c² = x² + (x - 7)²
17² = x² + x² - 14x + 49
2x² - 14x + 49 - 289 = 0
2x² - 14x - 240 = 0
d₁ = 7² - 2 * (-240) = 49 - (-480) = 529
d₁ > 0, уравнение имеет 2 корня.
x₁ = -(-7) + √529 / 2 = 7 + 23 / 2 = 30 / 2 = 15
x₂ = -(-7) - √529 / 2 = 7 - 23 / 2 = -16 / 2 = -8
второй корень уравнение не подойдет, т.к он имеет отрицательное значение, а длина не может быть отрицательным числом, значит x = 15.
a = 15
b = 15 - 7 = 8
p = 17 + 15 + 8 = 40 (см)
ответ: p = 40 (см)
