Дано :
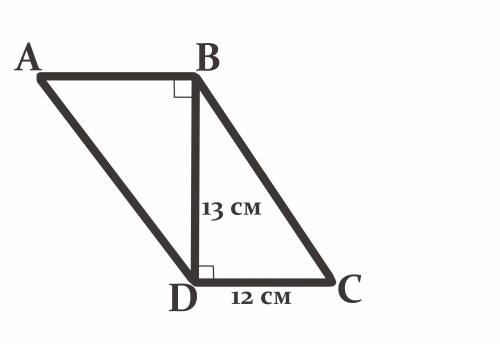
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
1.
Да,т.к. сумма углов этого 4-угольника равняется 360 градусам
2.
по формуле (n-2)*180 найдем сумму углов (8-2)*180=6*180=1080 градусов
один угол равняется 1080/n=1080/8=135 градусов
3.
d=n*(n-3)/2=9*(9-3)/2=9*6/2=27
ответ:27 диагоналей
4.
P=48 см
Пусть одна сторона x ,тогда другая x-4
Составим уравнение x+x+x-4+x-4=48
4x-8=48
4x=48+8
4x=56
x=14
ответ:14см
5.
Сумма углов параллелограмма прилежащих к одной стороне равняется 180 градусам,пусть один угол 2x,тогда другой угол 3x,составим уравнение
2x+3x=180
5x=180
x=36
тогда углы параллелограмма 2*36=72 и 3*36=108
ответ:72,108,72,108.
6.
∠BCO=∠OCD,т.к. диагональ AC делит ∠BCD по полам
Треугольник OCD прямоугольный,тогда ∠OCD=180-(90+63)=180-153=27
ответ:27 градусов
Объяснение:
S1=0.5*h*(0.5*b) - площадь KBC
S=2*S1=0.5*h*b - площадь ABC
треугольники CKB и ONB подобны
Значит (0.5*b)/h=r/(h-r)
b=(r*h)/(h-r)/0.5
Получили S=0.5*h*b=h*(r*h)/(h-r)
h=50 см, r=16 см