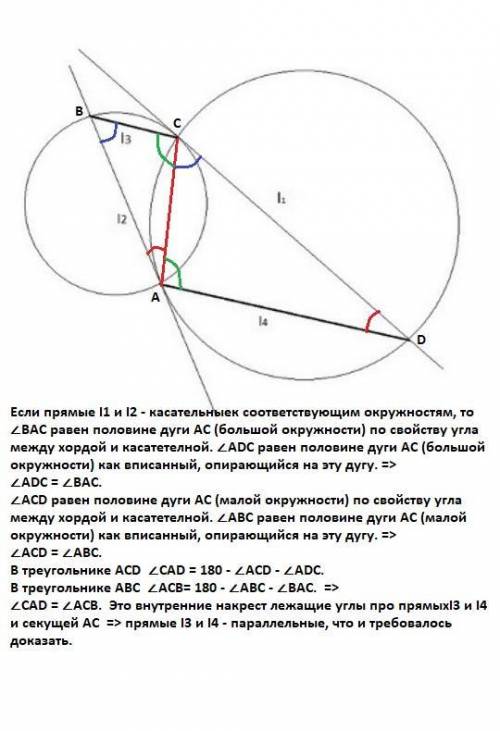
Доказательство в объяснении и приложении.
Объяснение:
Если прямые I1 и I2 - касательные к соответствующим окружностям, то ∠ВАС равен половине дуги АС (большой окружности) по свойству угла между хордой и касательной. ∠ADC равен половине дуги АС (большой окружности) как вписанный, опирающийся на эту дугу. =>
∠АDC = ∠ВАC.
∠ACD равен половине дуги АС (малой окружности) по свойству угла между хордой и касательной. ∠AВC равен половине дуги АС (малой окружности) как вписанный, опирающийся на эту дугу. =>
∠АСD = ∠ABC.
В треугольнике ACD ∠CАD = 180 - ∠АСD - ∠ADC.
В треугольнике AВC ∠АСВ= 180 - ∠АBC - ∠BAC. =>
∠CАD = ∠АСВ. Это внутренние накрест лежащие углы про прямыхI3 и I4 и секущей АС => прямые I3 и I4 - параллельные, что и требовалось доказать.
Доказательство в объяснении и приложении.
Объяснение:
Если прямые I1 и I2 - касательные к соответствующим окружностям, то ∠ВАС равен половине дуги АС (большой окружности) по свойству угла между хордой и касательной. ∠ADC равен половине дуги АС (большой окружности) как вписанный, опирающийся на эту дугу. =>
∠АDC = ∠ВАC.
∠ACD равен половине дуги АС (малой окружности) по свойству угла между хордой и касательной. ∠AВC равен половине дуги АС (малой окружности) как вписанный, опирающийся на эту дугу. =>
∠АСD = ∠ABC.
В треугольнике ACD ∠CАD = 180 - ∠АСD - ∠ADC.
В треугольнике AВC ∠АСВ= 180 - ∠АBC - ∠BAC. =>
∠CАD = ∠АСВ. Это внутренние накрест лежащие углы про прямыхI3 и I4 и секущей АС => прямые I3 и I4 - параллельные, что и требовалось доказать.

Из вершины угла А, равного 60°, проведена биссектриса АД.
Отрезок СД = 14 см.
Отрезок ВД обозначим х, а катет АВ - у.
Запишем тангенсы углов:
tg АВД = х/у,
tg САВ = (х + 14)/у.
По заданию имеем угол АВД = 30°, угол САВ = 60°.
Тогда х/у = 1/√3,
(х + 14)/у = √3.
Из первого уравнения у = х√3 подставим во второе:
(х + 14)/(х√3) = √3.
Получаем х + 14 = 3х, откуда 2х = 14 и х = 14/2 = 7 см.
Катет АВ = у = х√3 = 7√3 см.
ответ: катеты равны - АВ = 7√3 см, ВС = 7 + 14 = 21 см,
гипотенуза АС = √(147 + 441) = √588 = 14√3 см.