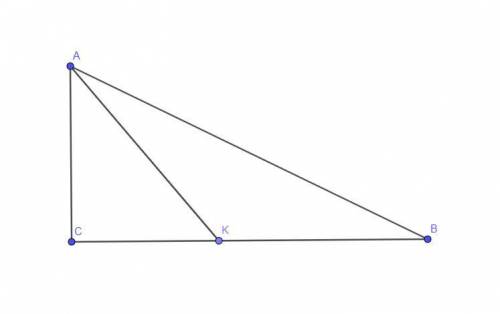
Угол C = 90 градусов.
Угол AKC = 60 градусов
KC = 4 см
Если угол AKC = 60 градусов, то из Теоремы о Сумме Углов треугольника найдем угол CAK:
CAK = 180 - (90+60) = 30 градусам.
Треугольник CAK - прямоугольный.
По свойству прямоугольного треугольника, напротив угла в 30 градусов (угла CAK), лежит катет равный 1/2 от гипотенузы.
т.е AK = CK * 2 = 8 см.
Если угол A равен 60 градусов, а угол CAK = 30 градусов, то угол KAB треугольника AKB равен 60 градусов - угол CAK = 60 - 30 = 30 градусов.
Угол AKB = 180 градусов - угол AKC (по теореме о смежных углах) = 180 - 60 = 120 градусов.
Угол KBA треугольника AKB по теореме о сумме углов треугольника, равен:
180 - (KAB + AKB) = 180 - (120 + 30) = 30 градусам.
У треугольника AKB углы при основании равны м-у собой.
По этому признаку его можно считать равнобедренным.
Его боковые стороны равны:
AK=KB=8 см.
Сторона треугольника BK равна 8 см.
Т.к. ∠ АОВ=∠ВОС=...=∠GОА=2π/7, то площадь одного из семи треугольников АОВ, ВОС,СОD, ...GОА может быть найдена как
0.5R²*sin2π/7, тогда площадь правильного семиугольника равна
3.5R²*sin2π/7=70⇒площадь искомой фигуры, состоящей из трех равных треугольников найдем так (3/7)(70)=30/см²/
да. еще раз. есть формула площади для треугольника.
это - половина произведения двух сторон на синус угла между ними. а 2π/7 - это центральный угол, а заодно и угол между данными сторонами. Нам нужно только увидеть. что таких треугольников равных семь, у правильного семиугольника, а нас интесуют только три из семи, т.е. 3/7 от 70
0 исходный отрезок (длина √2-1)
1 Из левого конца отрезка вертикально вверх прямую (как построить перпендикуляр к отрезку не описываю, надеюсь, сообразите, нет - добавятся ещё этапы)
2 окружность, центр на из левом конце отрезка, радиус равен длине отрезка (радиус √2-1)
3 из точки пересечения окружности пункта 2 и вертикальной прямой пункта 1 строим окружность, через правый конец исходного отрезка, радиус (√2-1)*√2 = 2-√2
----------------------
Расстояние от точки перечесения с вертикальной прямой окружности из пункта составляет 2-√2 + √2-1 = 1
И мы получили отрезок единичной длины, на котором можно строит ь квадрат
4, 5, 6 - достраиваем квадрат