Question

Нйдите площадь треугольника, две стороны которого равны 6 и 8, а медиана,заключённая между ними, равна 5.

Answer 1

Найдите площадь треугольника, две стороны которого равны 6 и 8, а медиана, заключённая между ними, равна 5.

▔ ▔ ▔

★☆★ Чертёж смотрите во вложении ★☆★

Дано:

ΔАВС.

АВ = 6.

ВС = 8.

ВО — медиана = 5.

Найти:

S(ΔАВС) = ?

Решение:

Достроим ΔАВС до параллелограмма ABCD как показано на рисунке.

▸Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам◂

Следовательно —

$BO = OD = 5.$

Тогда —

$DB = BO+OD\\\\DB = 5+5\\\\DB = 10.$

▸Противоположные стороны параллелограмма равны◂

AD и ВС — противоположные стороны.

Следовательно —

$AD=BC=8.$

Рассмотрим ΔABD.

▸Если сумма квадратов двух сторон равна квадрату большей стороны, то такой треугольник — прямоугольный (теорема, обратная теореме Пифагора)◂

Проверим стороны ΔABD —

$AD^{2} +AB^{2} = BD^{2}$

Подставим известные нам численные значения —

$8^{2} +6^{2} = 10^{2}\\\\64+36=100\\\\\boxed{100=100}$

Мы получили верное равенство, следовательно, ΔABD — прямоугольный (∡A = 90°).

▸Если в параллелограмме один угол прямой, то этот параллелограмм — прямоугольник◂

То есть, параллелограмм ABCD — прямоугольник.

Тогда, по определению прямоугольника —

∡А = ∡В = ∡С = ∡D = 90°.

Рассмотрим ΔАВС — прямоугольный.

▸Площадь прямоугольного треугольника равна половине произведения его катетов◂

Следовательно —

$\boxed{S(\triangle ABC)=\frac{AB*BC}{2} }$

Подставим в формулу известные нам численные значения —

$S(\triangle ABC)=\frac{6*8}{2} \\\\S(\triangle ABC)=\frac{48}{2} \\\\\boxed{S(\triangle ABC)=24}$

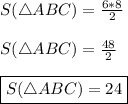
ответ:

24 (ед²).