Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.
Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольников со стороной 3 см.
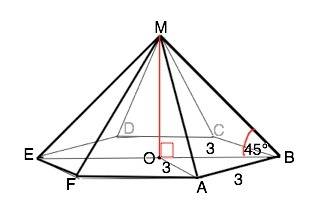
Обозначим пирамиду ABCDEF, центр - О.
Высота МО и половина ВО диагонали ВЕ образуют прямоугольный треугольник МОВ, острый угол МВО=45°. ⇒ Это равнобедренный треугольник, и МО=ВО=3 см.
Объём пирамиды равен 1/3 произведения высоты на площадь основания.
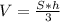
Площадь правильного шестиугольника – сумма площадей 6 правильных треугольников, площадь которых найдем по формуле:
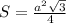
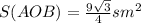
Площадь основания
6•9√3/4 sm²
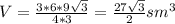
ответ:Вот
Объяснение:
Если у ромба угол равен 60 градусов, от меньшая диагональ равна стороне. Если угол, образованный меньшей диагональю с плоскостью основания, равен 45 градусов, то высота параллелепипеда равна меньшей диагонали основания, то есть равна его стороне. Поскольку у параллелограмма сумма квадратов сторон равна сумме квадратов диагоналей, то длина большей диагонали ромба равна 10 * √ 3 см. Тогда полная поверхность параллелепипедаSп = 2 * Sосн + 4 * Sб.гр. = 10 * 10 * √ 3 + 4 * 10² = 400 + 100 * √ 3 см²Меньшее дигональное сечение разбивает параллелепипед на 2 одинаковые правильные треугольные призмы, боковые грани которых – квадраты, поэтому сумма площадей их боковых поверхностейS = 6 * S б.гр. = 6 * 10² = 600 см²
В рівнобічній трапеції з вершин В і С опустимо перпендикуляри на сторону АD. ВС=HO, звідси AH+DO=AD-BC. Оскільки трапеція рівнобічна, то AH=DO, а отже
Розглянемо трикутник BHD. Оскільки BH перпендикуляр опущений на сторону АD, то кут BHD=90°, а отже трикутник BHD прямокутний, тому можна застосувати теорему Піфагора BD²=BH²+HD²HD=HO+ODHD=7+5=12BD=13BH²=BD²-HD²
Відповідь: площа трапеції 60 см².
Подробнее - на -