а)уравнение стороны AB = -8х+4у+84=0, BC=2х+14у-6=0, AC=-10х-10у-30=0. Можно представить эти уравнения с угловым коэффициентом в виде y = kx + a. Для этого перенесем все значения кроме y в правую часть, например: 4y = 8x - 84. Затем разделим правую часть на коэффициент 4. Получим: y = 2x - 21. б)уравнение высоты CH можно составить, зная координату точки Н(8;-5) СН = 6х+12у+12=0. в)уравнение медианы AM можно составить, зная координату точки М(3;0) АМ = -9х-3у+27=0. г)точку N пересечения медианы AM и высоты CH: так как заданный треугольник равнобедренный (а=в=14,1421), то высота на сторону АВ является и медианой. Поэтому точка N - центр тяжести треугольника. N(4;-3). д)уравнение прямой,проходящей через вершину C параллельно стороне AB = у-2х-9=0 или у = 2х+9. е)расстояние от точки C до прямой AB - это высота СН = 13,4164.
Подробно.
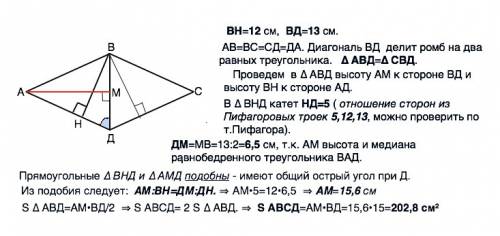
Пусть данный ромб АВСД.
Высота ВН=12 см, диагональ ВД=13 см.
Стороны ромба равны.
Диагональ ромба делит его на два равных треугольника.
∆ АВД=∆ СВД.
Проведем в равнобедренном ∆ АВД высоту АМ к стороне ВД и высоту ВН к стороне АД.
В ∆ ВНД катет НД=5 ( отношение сторон из Пифагоровых троек 5,12,13, можно проверить по т.Пифагора).
ДМ=МВ=13:2=6,5 см, т.к. АМ высота и медиана равнобедренного треугольника ВАД.
Прямоугольные ∆ ВНД и ∆ АМД подобны - имеют общий острый угол при Д.
Из подобия следует:
АМ:ВН=ДM:ДH.
АМ•5=12•6,5
AM=15,6 см
S ∆ АВД=АМ•ВД/2
S АВСД= 2 S ∆ АВД.
S АВСД=АМ•ВД=15,6•15=202,8 см²
ответ:17