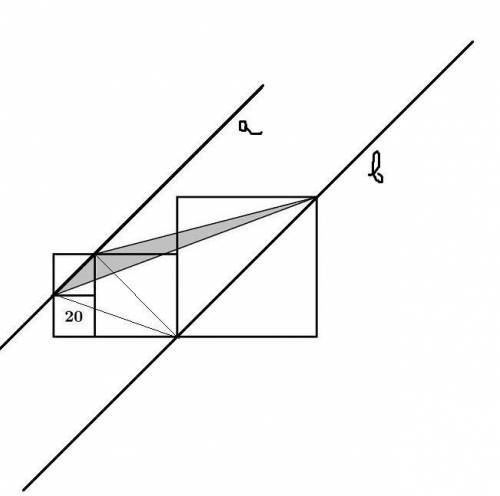
Рассмотрим множество треугольников, у которых две вершины расположены на диагонали маленького квадрата (на исходном рисунке в условии), а третья лежит на прямой, содержащей диагональ большого квадрата (см. мой рисунок). Заметим, что площади треугольников, входящих в это множество, попарно равны. Действительно, у всех треугольников общая сторона — диагональ малого квадрата, высоты, падающие на эту диагональ тоже равны, поскольку a ║ b.
Значит, площадь серого треугольника равна площади треугольника, указанного на моем рисунке. Площадь среднего квадрата равна 80. Теперь осталось следить за руками: (80+20+20)-40-10-60/2=70-30=40. Площадь равна 40.
АВ = 88-24 = 64 см
АЕ = АВ/2 = 32 см как катет против угла в 30°
ЕВ = √(АВ² - АЕ²) = √(64² - 32²) = 32√3 см по теореме Пифагора
рассмотрим ΔВЕР
ЕР = ЕВ/2 = 16√3 см как катет против угла в 30°
Площадь трапеции
S = 1/2(24+88)*16√3 = 896√3 см²