Объяснение:
Дана правильная треугольная пирамида. Её высота Н равна a√3, радиус окружности, описанной около её основания, равен 2a.
Найти: а) апофему А пирамиды.
Радиус R окружности, описанной около её основания, равен 2/3 высоты основания, то есть R = в√3/3, где в - сторона основания.
Находим сторону основания: в = R/(√3/3) = R√3 = 2a√3.
Отсюда апофема равна: А = √(Н² + (R/2)²) = √(3a² + a²) = √4a² = 2a.
Величина R/2 равна 1/3 высоты основания или радиусу вписанной окружности в основание.
б) угол α между боковой гранью и основанием равен:
α = arc tg(H/(R/2)) = arc tg(a√3/a) = arc tg√3 = 60 градусов.
в) площадь Sбок боковой поверхности.
Периметр основания Р = 3в = 3*2a√3 = 6a√3.
Sбок = (1/2)РА = (1/2)*(6a√3)*2а = 6a²√3 кв.ед.
г) плоский угол γ при вершине пирамиды(угол боковой грани).
γ = 2arc tg((в/2)/А) = 2arc tg((2а√3/2)/2а) = 2arc tg(√3/2) ≈ 1,42745 радиан или 81,7868 градуса.
Дано:
ABCDA₁B₁C₁D₁ - куб
AB = 2
--------------------------------
Найти:
а) р(B, A₁C₁) - ?
б) р(A, BD₁) - ?
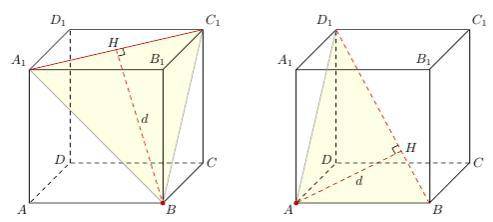
а) Проведем BH⊥A₁C₁. Искомое расстояние BH = d есть высота BH - ΔBA₁C₁. ΔA₁BC₁ равносторонний — все его стороны, будучи диагоналями граней, равны ⇒ A₁B = BC₁ = √2, cледовательно:
sin∠BA₁H → BH/BA₁ → BH = BA₁ × sin60° = √2 × √3/2 = √6/2 ⇒ BH = р(B, A₁C₁) = √6/2
(Рисунок показан внизу где влево).
б) Проведем BH⊥BD₁ Искомое расстояние AH = d есть высота AH - ΔABD₁. ΔABD₁ - прямоугольный. Действительно, прямая AB⊥(ADD₁) и поэтому перпендикулярна любой прямой, лежащей в этой плоскости — в частности, прямой AD₁.
Имеем: AB = 2, AD₁ = √2, BD₁ = √3
Если S — площадь треугольника ABD₁, то получаем:
2S = AB×AD₁ = BD₁×AH ⇒ AH = AB×AD₁/BD₁ = 2×√2/√3 = 2√2/√3 × √3/√3 = 2√2×3/(√3)² = 2√6/3 ⇒ р(A, BD₁) = AH = 2√6/3
(Рисунок показан внизу где вправо).
ответ: а) р(B, A₁C₁) = √6/2, б) р(A, BD₁) = 2√6/3
угол при вершине y,
y = 180 - 2x
а) сумма двух углов при основании
2x = 60
x = 30°
у = 120°
Такой треугольник возможен
в) сумма одного угла при основании и угла при вершине
x + y = 60
x + 180 - 2x = 60
120 = x
y = 180 - 240 = -60°
Это невозможный треугольник
ответ - 30°