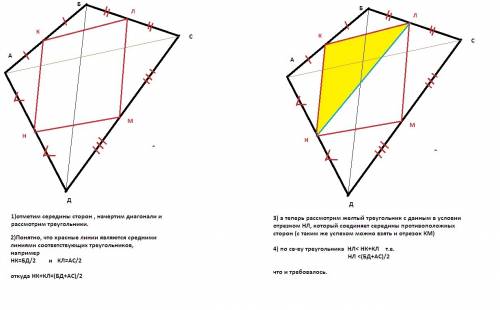
Рассмотрим четырехугольник ABCD; Пусть в нем диагональ AC зафиксирована, то есть имеет постоянную длину. Минимальная полусумма диагоналей получается тогда, когда вторая диагональ имеет нулевую длину. В таком случае точка B переходит в точку D. Рассмотрим отрезок MN - тот, что соединяет середины сторон BC и AD. Он сместился в точку M', причем MN ║ BD, поскольку B сместилась в D. Точка N осталась на прежнем месте. Получили треугольник ACD в котором M'N - средняя линия. Поэтому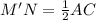 
, но мы рассматриваем четырехугольник, никакие две вершины которого не лежат друг на друге. Значит, в остальных случаях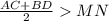 
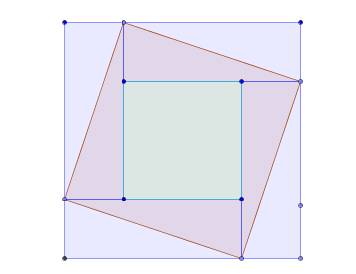
Пусть сторона большого квадрата 4х, тогда сторона зеленого квадрата 2х (с каждой стороны "отрезан" кусок стороной х)
Площадь большого квадрата S=16x^2, площадь зеленого квадрата 4x^2.
Заметим, что в каждом синем прямоугольнике площади делятся пополам, а в сумме площадь составляет (16-4)x^2=12 x^2, тогда для того, чтобы получить площадь второго квадрата, к площади зеленого квадратика нужно прибавить половину площадей прямоугольничков, т.е. S1=4x^2+(12x^2)/2=10x^2
Отношение площадей равно S/S1=16/10=8/5.
2) 450-2=448
3) 448+3=551
Если в пункте 2) минус изменить на плюс, то этот пример станет верным