В окружность вписана равнобедренная трапеция так, что ее большее основание является диаметром окружности. Боковые стороны ее равны 4√2. средняя линия равна 14. Найти радиус окружности.
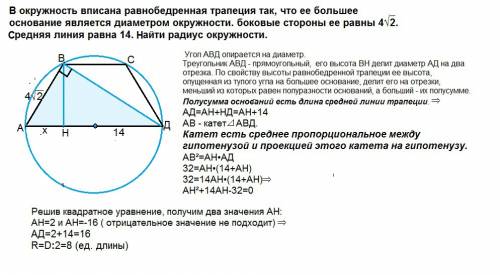
На рисунке, данном в приложении, АВСД - трапеция. АД - диааметр, АВ - боковая сторона трапеции.
Проведем диагональ ВД.
Угол АВД вписанный и опирается на диаметр, стягивающий дугу 180º. ⇒∠АВД=90º
Треугольник АВД - прямоугольный, его высота ВН делит диаметр АД на два отрезка. По свойству высоты равнобедренной трапеции ее высота, опущенная из тупого угла на большее основание, делит его на отрезки, меньший из которых равен полуразности оснований, а больший - их полусумме.
Полусумма оснований есть длина средней линии трапеции. ⇒
АД=АН+НД=АН+14
АВ - катет⊿ АВД. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу
АВ²=АН•AД
32=АН•(14+АН)
32=14АН•(14+АН)⇒
АН²+14АН-32=0
Решив квадратное уравнение, получим два значения АН:
АН=2 и аН=-16 ( отрицательное значение не подходит) ⇒
АД=2+14=16 - это длина диаметра окружности.
R=D:2=8 (ед. длины)
Рисуем треугольник ABC. Берем циркуль ставим его иголку в вершину A проводим окружность немного большего диаметра чем половина более длинной из примыкающей к ней сторон AB и AC. Потом не меняя диаметра ставим циркуль в вершину B и проводим окружность - через 2 точки пересечения второй и первой окружности проводим (при линейки и карандаша) линию. Повторяем эту же операцию для вершины D: проводим окружность с центром в D и через точки ее пересечения с первой окружностью - линию до пересечения с предыдущей линией. Пересечение этих двух линий - центр искомой описанной окружности. Ставим ножку циркуля в эту точку, раздвигаем ножки так, чтобы грифель через вершину A и проводим искомую описывающую окружность - она должна пройти через все три вершины треугольника.