
8см
Объяснение:
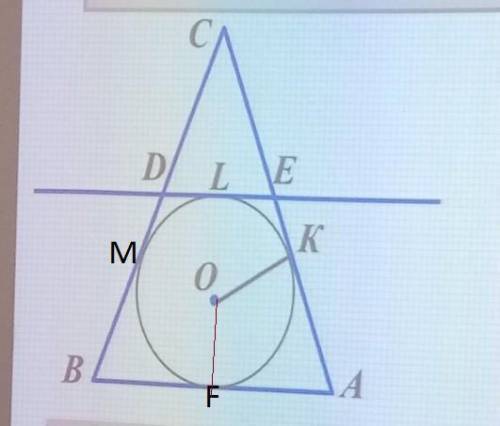
Теорема: Отрезки касательных к окружности, проведенные из одной точки, равны:
1) BM = BF MD = DL
FA = KA EK = LE
2) Pcde = CD + DE + CE =
= CD + (DL + LE) + CE = (CD + MD) + (EK +CE) = CM + CK =
= (BC - BM) + (AC - AK)
Т.к. ΔАВС - равнобедренный, то
ВС = АС = (Pabc - AB)/2 = (20 - 6)/2 = 7(cм)
Pcde = ВС + АС - ВМ - АК = 2 * 7 - ВМ - АК = 14 - ВМ - АК
3) Центр вписанной окружности лежит на биссектрисе. Но в равнобедренном треугольнике высота, а так же медиана и биссектриса, проведенные к основанию совпадают, следовательно, СF - медиана и делит АВ пополам:
ВF = FA = 6 / 2 = 3 (см)
4) Т.к. отрезки касательных к окружности, проведенные из одной точки, равны, то
BF = BM = 3(см)
FA = AK = 3(см)
Pcde = 14- ВМ - АК = 14 -2*3 = 8(см)
Сторона вписанного правильного многоугольника образует с радиусами описанной около него окружности равносторонний треугольник.
В нашем случае это треугольник с боковыми гранями, одинаковыми 43 и основанием, одинаковым 12см. По аксиоме косинусов найдем угол при верхушке этого треугольника:
Cos = (b+c-a)/2bc. ( - меж b и c). В нашем случае:
Cos=(2*(43)-12)/(2*43)=-48/(2*48)=-(1/2).
То есть центральный угол тупой и равен 120.
Как следует, число сторон нашего вписанного многоугольника равно 360/120=3. Это ответ.
P.S. Можно проверить по формуле радиуса описанной около правильного треугольника окружности: R=(3/3)*a. В нашем случае
R=(3/3)*12=43, что подходит условию задачки.
Напомним некоторые определения
Определение:
Окружностью с центром в точке О и радиусом R называют множество всех точек плоскости, удаленных от точки О на расстояние R (см. Рис. 1).
Рис. 1
Часть окружности называется дугой.
Дуга имеет угловое измерение.
Градусная мера дуги равна градусной мере соответствующего центрального угла :
Рассмотрим примеры:
Рис. 2
Определение
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным.
Рис. 3
Задана окружность с центром О, вершина А лежит на окружности, стороны АВ и АС угла пересекают окружность в точках В и С, угол называется вписанным. Он опирается на дугу , эта дуга расположена внутри угла (см. Рис. 3).
2. Теорема о вписанном углеВписанный угол измеряется половиной дуги, на которую он опирается (см. Рис. 4).
Рис. 4
Доказательство:
Рассмотрим несколько случаев.
Случай 1: точка О принадлежит лучу АС (см. Рис. 5).
Рис. 5
Доказать, что
Обозначим угол через , тогда угол также будет равен , так как треугольник равнобедренный, его стороны ОВ и ОА равны как радиусы окружности. Угол является внешним для треугольника , внешний угол равен сумме двух других углов, не смежных с ним, получаем: , то есть угловое измерение дуги есть . Таким образом, мы доказали, что вписанный угол равен половине измерения дуги, на которую он опирается.
Случай 2: точка О лежит внутри вписанного угла (см. Рис. 6).
Рис. 6
Доказать, что
Доказательство сводится к предыдущему случаю. Проведем диаметр AD, обозначим угол за и тогда дуга равна (объяснение см. случай 1). Угол за , тогда дуга равна (объяснение см. случай 1). Вся дуга равна:
Угол в свою очередь, равен .
Таким образом, мы доказали, что вписанный угол равен половине дуги, на которую он опирается.
Случай 3: точка О находится вне вписанного угла (см. Рис. 7).
Рис. 7
Доказать, что
Доказательство снова сводится к первому случаю. Проведем диаметр AD, обозначим угол через , тогда дуга (объяснение см. случай 1). Угол обозначим через , тогда дуга равна (объяснение см. случай 1). Дуга является разностью большой дуги и дуги :
Вписанный угол равен . Таким образом, мы доказали, что вписанный угол равен половине дуги, на которую он опирается.
Итак, теорема полностью доказана, все случаи рассмотрены. И теперь из этого вытекают важные следствия.
3. Следствия теоремы о вписанном углеСледствие 1:
Вписанные углы, опирающиеся на одну и ту же дугу, равны между собой (см. Рис. 8).
Рис. 8
Угол равен , он вписанный и опирается на дугу , значит, дуга равна . Но на эту же дугу опираются много других углов, например, углы и , данные углы измеряются половиной градусной меры дуги, значит, они равны , как и угол .
Таким образом, получаем:
Следствие 2
Вписанные углы, опирающиеся на диаметр, прямые (см. Рис. 9).
Рис. 9
Теорема о вписанном угле является ключом к доказательству многих других теорем и к решению многих задач.
4. Теорема о хордахПроизведение отрезков каждой из двух пересекающихся хорд есть величина постоянная.
Рис. 10
Доказать, что
Доказательство:
Рассмотрим треугольники и (см. Рис. 10). Данные треугольники подобны по равенству двух углов: равны вертикальные углы и ; вписанные углы и опираются на одну и ту же дугу . Выпишем соотношение подобия:
Применим свойство пропорции и преобразуем выражение:
, что и требовалось доказать.