Вариант для любителей тригонометрии
Объяснение:
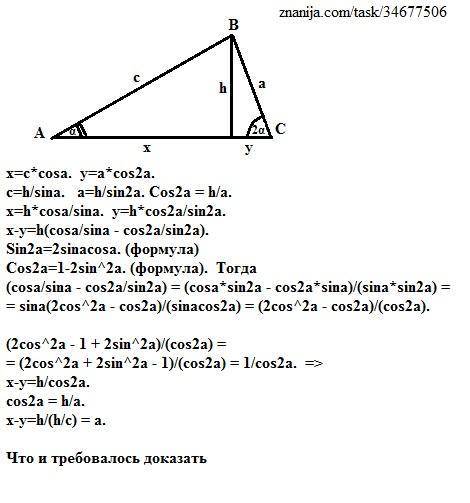
Дан треугольник АВС с основанием АС и высотой h, проведенной к основанию. Стороны треугольника
АВ = "с", ВС = "а".
Пусть основание делится высотой на отрезки, равные x и y, считая от вершины А. Тогда из прямоугольных треугольников, на которые высота делит исходный треугольник, имеем:
x = c*cosa. y = a*cos2a.
c = h/sina. a = h/sin2a. cos2a = h/а. =>
x = h*cosa/sina. y = h*cos2a/sin2a.
x - y = h(cosa/sina - cos2a/sin2a).
Sin2a = 2sina·cosa. (формула двойного аргумента)
Cos2a = 1 - 2sin²а. (формула двойного аргумента) Тогда
cosa/sina - cos2a/sin2a =
(cosa·sin2a - cos2a·sina)/(sina·sin2a). =>
sina(2cos²а - cos2a)/(sina·cos2a)=(2cos²а - cos2a)/(cos2a).
(2cos²а - 1 + 2sin²а)/(cos2a) =
(2cos²а + 2sin²а - 1)/(cos2a) = 1/cos2a. =>
x - y = h/cos2a. cos2a = h/а. =>
x - y = h/(h/а) = а.
Что и требовалось доказать.
Объяснение:
Средние линии треугольника - отрезки, соединяющие середины его сторон. Треугольник, образованный средними линиями, подобен исходному, поэтому отношение сторон обоих треугольников одинаково. Если стороны исходного треугольника а, b, c, то средние линии равны 0,5а, 0,5b и 0,5 с.
Соответственно, 0,5а:0,5b:0,5 с= а:b:с.
НО!
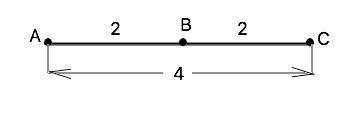
Треугольник с отношением сторон 2:2:4 не существует. По теореме . о неравенстве треугольника любая его сторона меньше суммы двух других. По данному отношению 4=2+2 все вершины лежат на одной прямой. (Треугольник, у которого все три вершины лежат на одной прямой, называется вырожденным - см. рисунок во вложении. ).
* * *
В сети встречается (и не раз!) задача, к которой дается решение без указания на неравенство треугольника, с таким условием:
Средние линии треугольника относятся как 2:2:4, а периметр треугольника равен 45 см. Найдите стороны треугольника. Ход решения верный, в ответе: а = b = 11,25; c = 22,5 см.
Получается, что с=а+b. Возможно, условие специально составлено так, чтобы решающий нашел в нем указанную выше ошибку.
ответ: 645 см