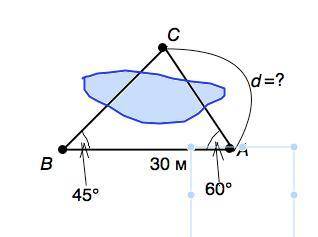
Объяснение: Чтобы найти расстояние d от пункта A до недоступного пункта C, на местности выбрали точку B и измерили длину с отрезка AB и углы α и β. Найдите расстояние от пункта A до пункта C, если AB = 30 м, α = 60°, β = 45°
————
Сделав рисунок по условию задачи, получим треугольник АВС с основанием АВ и углами ∠САВ=60° и ∠СВА=45°.
Из суммы углов треугольника ∠АСВ=180°-(45°+60°)=75°
По т.синусов АВ:sin75°=AC:sin45°.
Табличное значение sin75°= (√3+1)/2√2; sin45°=√/2 ⇒
30•2√2:(√3+1)=d:(√2/2) ⇒
AС=d= 60/(√3+1) или ≈ 21,96 м.
ответ:
1. р = 18см.
2 ас = 30/(√3+1) м.
объяснение:
площадь треугольника равна (1/2)·a·b·sinα, где a и b - стороны треугольника, а α - угол между этими сторонами. в нашем случае
а = 3х, b = 8x, sinα = √3/2. тогда
(1/2)·24х²·(√3/2) = 6√3 => x = 1 см.
имеем две стороны треугольника: 3см и 8см.
по теореме косинусов находим третью сторону:
х = √(3²+8²- 2·3·8·cos60) = √49 = 7см.
периметр треугольника равен 3+8+7 = 18см.
2. по теореме синусов в треугольнике авс:
ас/sinβ = ab/sinc.
∠c = 180 - 60 - 45 = 75°. sin75° = sin(45+30). по формуле
sin(45+30) = sin45·cos30 + cos45·sin30 = (√6+√2)/4.
тогда ас = ав·sinβ/sinc = (30·√3/2)/((√6+√2)/4). или
ас = 60/((√6+√2) = 60/(√2(√3+1)) = 30/(√3+1) м.
1) В правильной треугольной пирамиде проекции боковых рёбер на основание имеют угол между собой в 360°/3 = 120°.
Тангенс угла β наклона бокового ребра к основанию равен:
tg β = tg α*cos φ = tg 47*cos(120/2) = 1,07236871 * 0,5 = 0,536184355.
β = arc tg(0,536184355) = 0,492174352 радиан = 28,19951313°.
2) Проведём осевое сечение пирамиды через апофему.
В сечении - равносторонний треугольник.
Высота из середины основания этого треугольника на боковую сторону равна 2 см ( по заданию - это расстояние от центра основания до боковой грани).
Высота Н пирамиды как гипотенуза в 2 раза больше катета, лежащего против угла в 30°: Н = 2*2 = 4 см.
Апофема А равна стороне а основания: A = а.
По Пифагору А² = (а/2)² + Н²,
а² = (а/2)² + 4².
4а² = а² + 16*4,
3а² = 64,
а = √(64/3) = 8/√3 = 8√3/3 см.
Периметр основания Р = 4а = 4*(8√3/3) = 32√3/3 см.
Искомая площадь боковой поверхности пирамиды равна:
Sбок = (1/2)РА = (1/2)*(32√3/3)*(8√3/3) =128/3 = 42(2/3) см².