Даны две концентрические окружности. хорда большой окружности имеет длину 40 см и касается меньшей окружности. найти радиус большой окружности , если ширина кольца между этими окружностями равна 10 см

👇

Ответ:

artem28

24.03.2022

CB = AB/2 = 40/2 = 20
Из треугольника COB:
OB^2 = OC^2 + CB^2
R^2 = r^2 +20^2
Понятно, что:
R - r = 10
Получаем систему уравнений:
R^2 = r^2 +20^2 (1)
R - r = 10 (2)
Из уравнения (2) r = R - 10
Подставляем в уравнение (1):
R^2 = (R - 10)^2 + 400 = R^2 - 20R + 100 + 400
Сокращаем, и получаем:
20R = 500
R = 25 см
ответ: радиус большей окружности R = 25 см

Даны две концентрические окружности. хорда большой окружности имеет длину 40 см и касается меньшей о

Даны две концентрические окружности. хорда большой окружности имеет длину 40 см и касается меньшей о

4,7(54 оценок)

Открыть все ответы

Ответ:

ната1187

24.03.2022

ПО ТАКОМУ ПРИНЦИПУ

Диагональ куба равна 9 см.Найдите площадь его полной поверхности.

Пусть x - сторона куба. Площадь полной поверхности куба равна сумме площадей граней. Грани представляют из себя квадраты. Площадь квадрата см. Граней куба 6, поэтому площадь полной его поверхности см

Обозначим куб буквами ABCDA1B1C1D1, где ABCD - нижнее основание. Рассмотрим треугольник ABD. Найдем сторону BD. По теореме Пифагора

Рассмотрим треугольник DBB1, DB1=9см.

Находим площадь полной поверхности куба

см

ответ: площадь полной поверхности куба 162см

4,8(85 оценок)

Ответ:

Вероника1306

24.03.2022

Периметр 20-угольника равен 20 * 21, тогда точки делят периметр на отрезки длины 20 * 21/21 = 20 < 21. Значит, найдётся сторона 20-угольника, содержащая две точки 21-угольника.

Пусть C1C2C3...C21 - 21-угольник, A1A2A3...A20 - 20-угольник, и точки C1 и C20 лежат на A20A1. Обозначим C1A1 = 1 - x, тогда A1C2 = 19 + x, C2A2 = 2 - x, A2C3 = 18 + x, ..., C20A20 = 20 - x, A20C21 = x. Очевидно, 0 ≤ x ≤ 1.

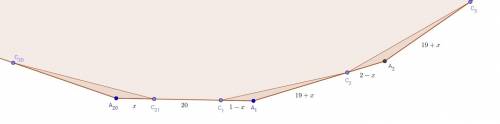
Разность площадей 20-угольника и 21-угольника равна сумме площадей треугольников C1A1C2, C2A2C3, C3A3C4, ..., C20A20C21. Так как все углы C1AC2, ..., C20A20C21 равны между собой и равны 180° - 360°/20 = 180° - 18°, то сумма площадей равна
S = 1/2 sin(180° - 18°) * ((1 - x)(19 + x) + (2 - x)(18 + x) + ... + (20 - x) x) = sin 18° ((1 - x)(19 + x) + (2 - x)(18 + x) + ... + (20 - x)x)/2

S(x) - квадратный трёхчлен относительно x, старший коэффициент отрицателен, поэтому максимум достигается в вершине квадратичной параболы. Так ка S(x) = S(1 - x), то парабола S(x) симметрична относительно x = 1/2, а значит, максимальное значение равно S(1/2).

Осталось вычислить значение. Выписываю сумму произведений в скобках:
0,5 * 19,5 + 1,5 * 18,5 + 2,5 * 17,5 + ... + 19,5 * 0,5 = (10 - 9,5)(10 + 9,5) + (10 - 8,5)(10 + 8,5) + ... + (10 - 0,5)(10 + 0,5) + (10 + 0,5)(10 - 0,5) + ... (10 + 9,5)(10 - 9,5) = 20 * 10² - 2 * 0.5² (1² + 3² + 5² + ... + 17² + 19²) = 2000 - 0.5 * 1330 = 1335
1² + 3² + ... + 19² можно посчитать вручную на листочке.

S(0.5) = 1335 sin18° / 2 - максимальное значение.

Вершины выпуклого 21-угольника расположены на сторонах правильного 20-угольника со стороной 21 так,