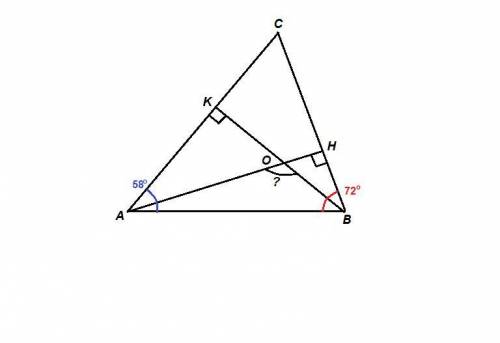
130°
Объяснение:
Сумма острых углов прямоугольного треугольника равна 90°.
ΔАНВ: ∠ АНВ = 90°,
∠ВАН = 90° - ∠АВН = 90° - 72° = 18°
ΔВКА: ∠ВКА = 90°,
∠АВК = 90° - ∠ВАК = 90° - 58° = 32°
ΔАОВ:
∠АОВ = 180° - (∠ВАО + ∠АВО) = 180° - (18° + 32°) =
= 180° - 50° = 130°
Из ΔАВС:
∠С = 180° - (∠А + ∠В) = 180° - (58° + 72°) = 180° - 130° = 50°
Сумма углов выпуклого четырехугольника равна 360°.
Для четырехугольника СКОН:
∠КОН = 360° - (∠С + ∠К + ∠Н) = 360° - (50° + 90° + 90°) =
= 360° - 230° = 130°
В треугольнике ABC AC=CB=10см, угол A=30 градусов, BK- перпендикуляр у плоскости треугольника и равен 5 см. Найти расстояние от K до AC
Рассмотрим образованную пирамиду АВСК. КВ перпендикулярно АВС, значит нам необходимо найти длину высоты, опущенной в грани АСК из вершины К на АС. По теореме о трех перпендикулярах ее проекция на плоскость АВС будет перпендикулярна АС. Обозначим точку пересечения высоты с АС через Н. Тогда нужно найти КН.
Рассмотрим основание пирамиды - треугольник АВС. Он равнобедренный АС=ВС=10, с углом у основания А=30 градусов. Опустим высоту из вершины треугольника С на АВ - СМ. Высота, опущенная из точки С, будет и биссектрисой, и медианой треугольника. То есть АМ=МВ. Треугольник АСМ - прямоугольный, с одним из осмтрых углов = 30 градусов, значит катет, лежащий против этого угла, равен половине гипотенузы: АМ=1/2*АС, АМ=1/2*10=5 (см) . По теореме Пифагора найдем второй катет СМ:
CM=sqrt(AC2-AM2)
CM=sqrt(100-25)=sqrt75=5sqrt3
BH- проекция КН на плоскость основания АВС, и, как было уже отмечено, ВН перпендикулярна АС. Рассм отрим треугольники АНВ и АМС- они подобны:
АН/АМ=НВ/МС=АВ/АС
НВ/МС=АВ/АС
НВ=МС*АВ/АС
НВ=5*(2*5sqrt3)/10=5sqrt3
Треугольник КНВ - прямоугольный (КВ перпендикулярно плоскости АВС) . По теореме Пифагора найдем КН:
KH2=KB2+HB2
KH=sqrt(25+75)=sqrt100=10 (см)