Данные точки лежат на поверхности шара, следовательно, не лежат на одной прямой.
Через любые три точки пространства, не лежащие на одной прямой, можно провести одну и только одну плоскость. Относительно к шару эта плоскость будет сечением, а сечение шара - круг.
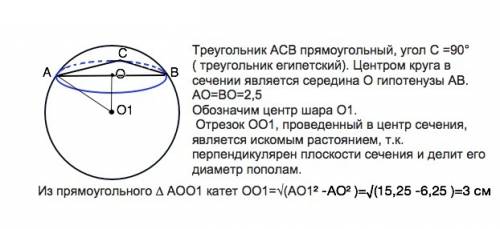
Соединив данные точки, получим треугольник АСВ, причем угол С =90° ( треугольник египетский). Тогда центром круга в сечении является середина О гипотенузы АВ.
r=АО=ВО=2,5
Обозначим центр шара О1.
Отрезок, проведенный в центр сечения, является искомым расстоянием, т.к. перпендикулярен плоскости сечения и делит его диаметр пополам.
Из прямоугольного ∆ АОО1 катет
ОО1=√(AО1² -АО² )=√(15,25 -6,25 )=√9=3 см
Угол при основании Ф. (обозначим)
Угол BAC = Ф, угол DAC = Ф/2;
Угол ADB = угол ВСА + угол DAC (И то и другое равно 180 минус угол ADC)
110 = Ф + Ф/2; Ф = 220/3, угол при вершине 100/3 (в градусах)