1. в параллелограмме abcd сторона cd равна 3 см,
диагонали равны 7 см и 4 см, о - точка пересечения
диагоналей. чему равен периметр треугольника аов?
2. в параллелограмме один угол равен 44°. найдите
остальные углы параллелограмма.
3*. в треугольнике abc /a = 50°. из точки, взятой
на стороне bc, проведены две прямые, параллельные сто-
ронам ab и ac. определите вид получившегося четырех-
угольника и все его углы.
вариант 2
1. в параллелограмме abcd диагонали равны 8 см и
5 см, сторона вс равна 3 см, 0 — точка пересечения диа-
гоналей. чему равен периметр треугольника аор?
2. в параллелограмме один из углов равен 144°. най-
дите остальные углы параллелограмма.
3*. из точки, взятой на одной из сторон равносторон-
него треугольника, проведены две прямые, параллельные
другим его сторонам. определите вид получившегося
четырехугольника и все его углы
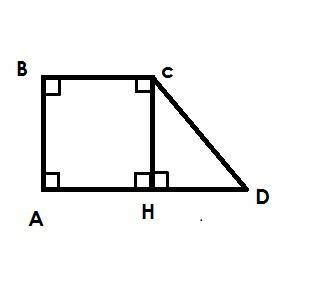
SinD=EP/HD => EP=DH*SinD.
SinD=GP/HC => GP=HC*SinD.
PH=√(GP*PE), как высота из прямого угла (<GHE=90°, так как опирается на диаметр GE). Тогда PH=SinD√(HD*CH).
Но √(HD*CH)=OH - высота из прямого угла в прямоугольном треугольнике СOD c <COD=90° (свойство трапеции: "В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°"). А так как ОН=АВ/2=R, то РН=(АВ/2)*SinD.
Площадь четырехугольника EFGH равна сумме площадей треугольников EFG и EHG.
Sefg=(1/2)*EG*OF = (1/2)*AB*(1/2)AB=AB²/4.
Sehg=(1/2)*EG*PH = (1/2)*AB*(AB/2)*SinD=AB²*SinD/4.
Тогда площадь четырехугольника EFGH равна (AB²/4)*(1+SinD).
Площадь трапеции равна (1/2)*(BC+AD)*AB. Но поскольку в трапецию вписана окружность, то ВС+АD=АВ+СD (свойство: "В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон").
В треугольнике CDK: CK=CD*SinD, но СК=АВ, значит CD=AB/SinD.
Тогда Sabcd=(1/2)*(AB+AB/SinD)*AB =AB²*(1+1/sinD)/2.
По условию Sabcd=4*Sefgh. или (АВ²*(1+1/sinD)/2=4*(AB²/4)*(1+SinD).
Отсюда 1/SinD==2 и SinD=1/2.
ответ: острый угол D трапеции равен 30°.