Средняя линия трапеции равна полусумме оснований
(16+26)/2 = 42/2 = 21 см
НА ПОУЧИ, НЕУЧ!
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
Коллинеарные вектора
рис. 1
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Найдем их векторное произведение
a × b =
i j k
ax ay az
bx by bz
= i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) =
= i (aynaz - aznay) - j (axnaz - aznax) + k (axnay - aynax) = 0i + 0j + 0k = 0
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
ax = ay .
bx by
Значит:
Вектора a и b коллинеарны т.к. 1 = 2 .
4 8
Вектора a и с не коллинеарны т.к. 1 ≠ 2 .
5 9
Вектора с и b не коллинеарны т.к. 5 ≠ 9 .
4 8
Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
n = by = 6 = 2
ay 3
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}
Так как b = na, то вектора a и b коллинеарны.
Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
ax = ay .
bx by
Значит:
3 = 2 .
9 n
Решим это уравнение:
n = 2 · 9 = 6
3
ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
ax = ay = az .
bx by bz
Значит:
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
n = by = 6 = 2
ay 3
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Так как b = na, то вектора a и b коллинеарны.
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
ax = ay = az .
bx by bz
Значит:
3 = 2 = m
9 n 12
Из этого соотношения получим два уравнения:
3 = 2
9 n
3 = m
9 12
Решим эти уравнения:
n = 2 · 9 = 6
3
m = 3 · 12 = 4
9
ответ: вектора a и b коллинеарны при n = 6 и m = 4.
1.
Пусть дан ABCD - прямоугольник, SАВСD = 15 см, АВ = 5 см.
Найдём ВС - ?
По формуле для Sпрямоуг = a×b ⇒ Sпрямоуг = AB×BC
BC=Sпрямоуг /AB
ВС=15/5 = 3 см
ответ : ВС = 3 см
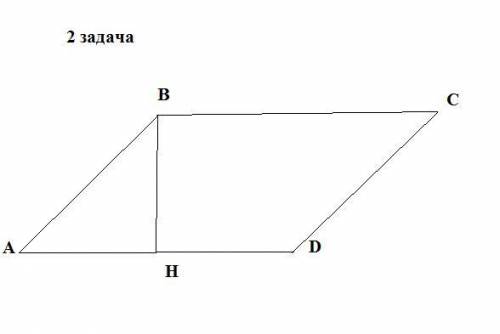
2.
Пусть дан параллелограмм ABCD,∠В= 150°, две стороны 12 и 16 см. Найдём SABCD -?
Из вершины В проведём высоту ВН к стороне АД.
∠А = 180° - ∠В = 180° - 150° = 30°.
Рассмотрим △АВН : ВН является высотой и катетом и находится против ∠30°.
АВ-гипотенуза , значит ВН = АВ : 2 = 12 : 2 = 6 см.
SABCD = ВН × АД = 6 × 16 = 96 см².
ответ : SABCD = 96 см²
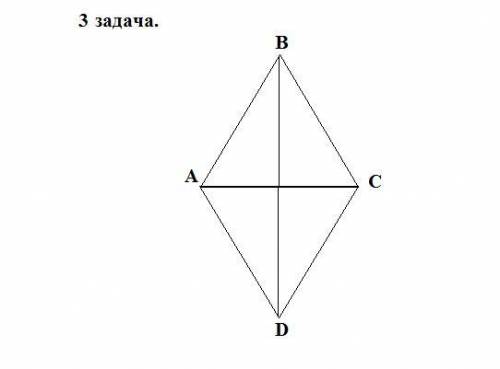
3.
Пусть дан ромб АВСD , АС- диагональ , ∠АСD = 35° .Найдём ∠АВС - ?
АС - биссектриса, ∠АСD = ∠ВАС = 35°, как накрестлежащие.
Рассмотрим △АВС : равобедренный, т.к у ромба все стороны равны, значит углы при основании равны.
∠АВС=180° - 35° - 35° = 110°
ответ : 110°
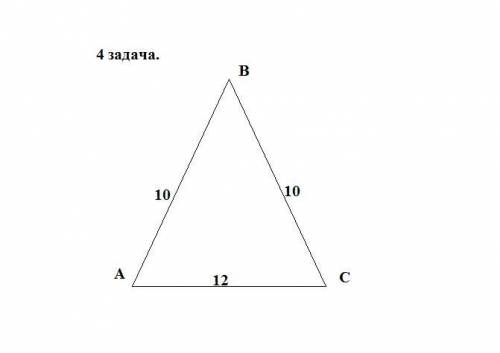
4.
Пусть дан △АВС-равнобедренный , АС-основание = 12 см.
АВ=ВС=10 см. Найдём S△АВС-?
Рассмотрим △АВС : Проведем высоту ВН , △АВС-равнобедренный ⇒ ВН является высотой , медианой и биссектрисой. Образован прямоугольный треугольник АВН, АН = НС = 12/2 = 6 см.
По теореме Пифагора найдём катет ВН :
ВН=√АВ² - АН²
ВН=√64
ВН=8 см
S△АВС=(ВН×АС)/2
S=(8×12)/2
S=48 кв. см
ответ:48 кв.см.
6.
2,4

21см (26+16):2 это все деление. Первое-это ответ