Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
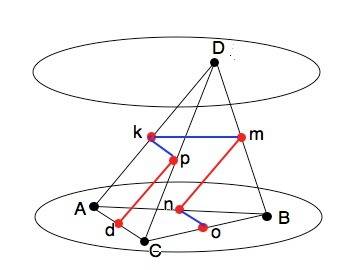
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
1) Прямая и плоскость могут иметь одну общую точку. ВЕРНО
Прямая пересекает плоскость.
2) Прямая и плоскость могут иметь три общие точки. ВЕРНО
Когда прямая лежит на плоскости, то каждая ее точка принадлежит этой плоскости, и три общие точки найдутся наверняка.
3) Прямая и плоскость могут не иметь общей точки. ВЕРНО
Тот случай, когда прямая параллельна плоскости.
4) Прямая и плоскость могут иметь только две общие точки. НЕВЕРНО
Прямая и плоскость могут не иметь общих точек, иметь одну общую точку либо бесконечное множество общих точек.