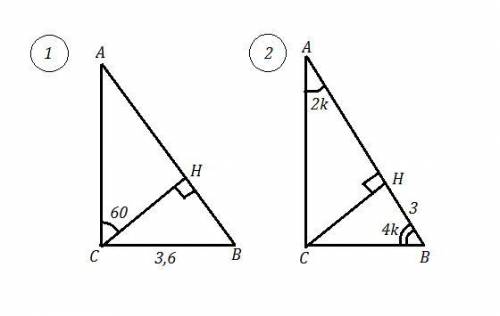
1) ΔАВС , ∠С=90° , СН⊥АВ , ∠ АСН=60°, ВС=3,6 см . Найти: АВ=?
Рассм. ΔАСН. ∠А=90°-∠АСН=90°-60°=30° .
Рассм. ΔАВС. Катет ВС=3,6 см лежит против угла в 30°, значит он равен половине гипотенузы, то есть ВС=1/2*АВ ⇒ АВ=2*ВС ,
АВ=2*3,6=7,2 (см) .
ответ: АВ=7,2 см .
2) ΔАВС , ∠С=90° , ∠С:∠А=4:2 , СН⊥АВ , ВН=3 см . Найти АН .
∠А+∠С=90° , ∠С=4k , ∠A=2k , 4k+2k=90° , 6k=90° , k=15° .
∠C=4*15°=60° , ∠A=2*15°=30° .
Рассм. ΔВСН. ∠ВНС=90° , ∠ВСН=90°-∠В=90°-60°=30° .
Катет ВН=3 см лежит против угла в 30°, тогда гипотенуза в 2 раза больше этого катета: ВС=2*3=6 см.
Из теоремы Пифагора: СН=√(ВС²-ВН²)=√(36-9)=√27=3√3 (см)
Рассм. ΔАСН. ∠АНС=90° , ∠А=30° ⇒ катет СН лежит против угла
в 30° ⇒ АС=2*СН=2*3√3=6√3 (см) .
АН=√(АС²-СН²)=√(36*3-9*3)=√81=9 (см)
ответ: АН=9 см .
Основание равнобедренного треугольника АВС - сторона ВС, так как прямая,параллельная основанию равнобедренного треугольника АВС пересекает стороны АВ и АС в точках М и N на сторонах АВ и АС по условию. Значит <ABC=<ACB как углы при основании.
Углы <AMN=<ABC и <ANM=ACB как соответственные углы при параллельных прямых MN и BC и секущих АВ и АС соответственно. Следовательно, треугольник MАN равнобедренный с основанием MN, так как углы при стороне MN равны между собой.
Что и тоебовалось доказать.
Пусть дана трапеция АВСD. Проведем высоту ВН. Высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований (свойство). АН=(18-12):2=3см. Тогда высоту ВН найдем по Пифагору из прямоугольного треугольника АВН:
ВН =√(АВ²-АН²) = √(17²-3²) = 2√70см. Площадь трапеции равна
S=(AD+BC)*BH/2 =30√70 см².