BC = 16/(2√3 - 1) см.
Объяснение:
Треугольник АВС равнобедренный, медиана ВК является и высотой, и биссектрисой. (см. рисунок в задании).
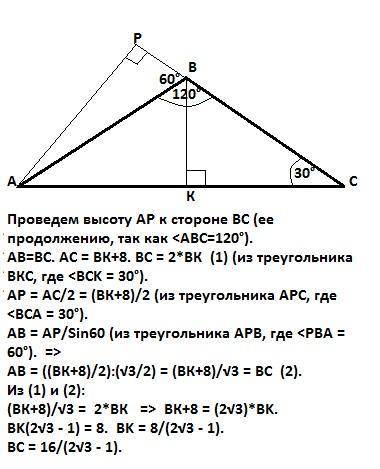
Проведем высоту АР к стороне ВС (ее продолжению, так как ∠<ABC=120°), АВ=ВС, АС = ВК+8см (дано).
ВС = 2*ВК (1) (из треугольника ВКС, где ∠BKC=90°, a ∠BCK=30°).
АР = АС/2 = (ВК+8)/2 (из треугольника АРС где ∠APC=90°, a ∠BCA=30°).
АВ = АР/Sin60 (из треугольника АРB, где ∠APB=90°, a ∠РBA=60°, а
Sin(∠PBA = AP/AB). Sin60 = √3/2 =>
АВ = ((ВК+8)/2):(√3/2) = (ВК+8)/√3 = ВС (2).
Из (1) и (2):
(ВК+8)/√3 = 2*ВК => ВК+8 = (2√3)*BK.
BK(2√3 - 1) = 8. BK = 8/(2√3 - 1).
BC = 16/(2√3 - 1)см.
Находим углы по заданному отношению. Т.к. отношение внеш1/3внутр, а многоугольник правильный, значит все внешние углы будут равны 360/4=90, а значит все внутренние 360-90=270.
Находим, сколько сторон имеет многоугольник:
Каждый внутренний угол многоугольника=180*(n-2)/n=270,
отсюда 270n=180n-360,
90n=360,
n=4.(сторон)
Проверяем по суммам и соотношению: 90*4/270*4 = 1/3
Правда я не понимаю, каким боком тут получается квадрат, который в любом случае будет иметь внутренние углы 90, а внешние 270. Ну ладно, условие таково. Если не возвращаться к самому исходу для чертёжной проверки, будет спокойнее.
Итак.
a) Как описано выше, многоугольник имеет 4 стороны.
б) Две диагонали.
в) 90 градусов.