Таким образом мы нашли один из углов при пересечении диагоналей (угол AEB) параллелограмма ABCD и он равен 53 градусам. Другой угол при пересечении (угол AED) является смежным к этому (к углу AEB) и следовательно равен 180 - 53 = 127 градусов. Оставшиеся два угла при пересечении (углы CED и BEC) являются вертикальными к уже найденным и равны 53 и 127 градусов соответственно. Меньшим из этих углов является угол 53 градуса, что и будет ответом к задаче.
а) 9,(4) + 1,(2) = 9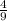 + 1
+ 1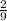 = 10
= 10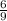 = 10
= 10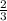
б) 2,(34) + 0,(21) = 2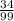 +
+ 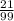 = 2
= 2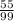 = 2
= 2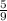
в) 19,(27) - 3,(73) = 19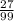 - 3
- 3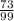 = 15
= 15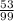
г) 6,(5)*18 = 6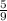 *18 =
*18 = 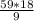 = 59*2 = 118
= 59*2 = 118
д) 8,1(6):2 = 8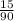 :2 =
:2 = 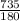 = 4
= 4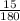 = 4
= 4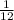
е) 1,(645) – 4,(001) = 1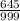 - 4
- 4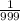 =
= 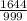 -
- 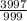 = -
= -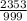 = -2
= -2