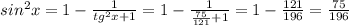
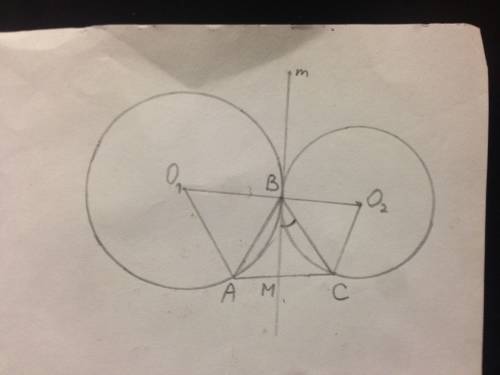
Меньшая окружность проходит через 3 вершины, одна из который - острый угол, а две - вершины тупых углов. Острый угол является вписанным в эту окружность. И, наоборот, большая окружность проходит через вершину острого угола, потом- тупого, и - опять острого. В большую окружность вписан тупой угол.
r = 3; R = 4; a = ?
Обозначим за Ф половину тупого угла ромба. В треугольнике, вписанном в малую окружность, это будет острый угол, противолежащий стороне а;
Тогда по теореме синусов
a = 2*r*sin(Ф); sin(Ф) = a/(2*r);
Для тупоугольного равнобедренного треугольника, вписанного в большую окружность, угол при основании (противолежащий стороне а) равен (180 - 2*Ф)/2 = 90 - Ф;
Поэтому по той же теореме синусов
a = 2*R*sin(90 - Ф) = 2*R*cos(Ф); cos(Ф) = a/(2*R);
Осталось возвести это в квадрат и сложить
1 = a^2/(2*r)^2 + a^2/(2*R)^2; (2/a)^2 = 1/r^2 + 1/R^2;
Подставляем r = 3; R = 4; получаем а = 24/5
1. Построим прямоугольник АВСД с точкой пересечения диагоналей О. Проведем из вершины С перпендикуляр к диагонали ВД и поставим точку Н в точке пересечения. По условиям задачи, перпендикуляр СН делит угол ВСД в отношении 3:1, отсюда следует, что угол НСД равен 22,5 градуса, а НСВ =67,5. Рассмотрим треугольник ВСН, в нем угол при вершине Н=90 град, при вершине С=67.5, тогда угол при вершине В (угол НВС)=22,5. Угол НВС= углу АСВ=22,5. Искомый угол ОСН = угол НСВ-ОСН=67,5-22,5=45