Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=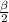
.
ΔАОК- прямоугольный ,
cos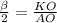
, KO=R*cos;
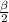sin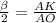
,AK=R*sin 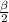,AB=α2Rsin .
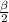ΔSKO прямоугольный ,cos α=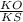
, KS=R*cos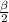/cosα.
S=0,5*AB*SK ,S=0,5*2R*sin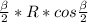
/ cosα,
S=0,5*R²*sinβ/cosα=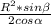
Трапеция АВСД, ВС=16, АД=30, точка О ниже АД, соединяем вершины трапеции с центром О, ОА=ОВ=ОС=ОД=17, в треугольнике ВСО проводим высоту ОК , треугольник ВСО равнобедренный, ОВ=ОС=17, ОК - медиана, биссектриса, высота. ВК=СК = 16/2=8
треугольник ОВК прямоугольный, ОК=корень(Ов в квадрате - ВК в квадрате) =
=корень =(289-64)=15
Треугольник ОАД равнобедренный , точка Н - пересечение ОК с АД, высота ОД=медиане биссектрисе, АН=ДН=30/2=15
треугольник ОАН прямоугольный, ОН= корень (АО в квадрате - АН в квадрате)=
=корень(289-225) = 8
КН - высота трапеции = ОК-ОН=15-8=7
1. В ΔАВС:
2. В ΔABD: