Против меньшего угла лежит меньшая сторона, поэтому самый маленький угол лежит против стороны в 10 см. Обозначим искомый угол как и применим теорему косинусов:
Из прямоугольного треугольника ВАН: sin ВАН = BH/AB = 5√3/10 = √3/2 Значит ∠ВАН = 60°. ∠ВСА = ∠ВАС = 60° как углы при основании равнобедренного треугольника. ∠АВС = 180° - 2·60° = 60°
ответ: все углы треугольника по 60°.
Из прямоугольного треугольника АВН по теореме Пифагора: АН = √(АВ² - ВН²) = √(100 - 25·3) = √(100 - 75) = √25 = 5 см Катет АН равен половине гипотенузы АВ, значит ∠АВН = 30°. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой, тогда ∠АВС = 60°.
Против меньшего угла лежит меньшая сторона, поэтому самый маленький угол лежит против стороны в 10 см. Обозначим искомый угол как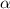
и применим теорему косинусов: