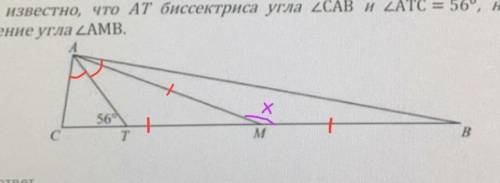
Так как точка М – середина ВС, то АМ – медиана ∆АВС, а СМ=МВ,
АМ=СМ по условию, получим что СМ=МВ=АМ.
Треугольник является прямоугольным, если его медиана делит противоположную сторону на отрезки, равные себе.
Следовательно ∆АВС – прямоугольный с прямым углом САВ.
АТ – биссектриса угла САВ по условию, следовательно угол САТ=угол САВ÷2=90°÷2=45°.
В треугольнике сумма всех углов равна 180°.
Тогда: угол АСТ=180°–угол САТ–угол АТС=180°–45°–56°=79°;
Угол АВС=180°–угол САВ–угол АСВ=180°–90°–79°=11°.
Так как АМ=МВ, то ∆АМВ – равнобедренный с основанием АВ.
Углы при основании равнобедренного треугольника равны.
Значит угол МАВ=угол МВА=11°.
Так как сумма всех углов в треугольнике равна 180°, то угол АМВ=180°–угол МАВ–угол МВА=180°–11°–11°=158°.
ответ: 158°
Площадь трапеции ABCE равна 18 кв. единиц
Пошаговое объяснение:
Отметим середину стороны АВ через F (см.). Тогда отрезок EF делит параллелограмм ABCD на два равные параллелограммы AFED и FECB. В параллелограмме AFED отрезок AE будет диагональю. В параллелограмме FECB также проведём диагональ EB. По свойству параллелограмма диагонали делят площадь параллелограмма на 2 равные треугольники. В итоге получаем 4 равные треугольники. Если площадь треугольника ADE равна 6 кв. единиц, то площадь трапеции ABCE равна 3·6=18 кв.единиц.
Даны координаты середин сторон треугольника АВС: M(3;-2;5, N (3,5;-1;6), K(-1,5;1;2).
Две половины сторон треугольника АВС и два стороны треугольника MNK образуют параллелограмм.
Поэтому координаты точки А симметричны точке К относительно середины отрезка MN как конец диагонали АК параллелограмма ANKM.
Аналогично вершины В и С.
Находим координаты середин отрезков:
О = (1/2)MN = ((3 + 3,5)/2=3,25; (-2-1)/2=-1,5; (5+6)/2=5,5) = (3,25; -1,5; 5,5).
Р = (1/2)NK = ((3-1,5)/2=0,75; (-2+1)/2=-0,5; (5+2)/2=3,5) = (0,75; -0,5; 3,5).
Т = (1/2)MK = (3,5-1,5)/2=1; (-1+1)/2=0; (6+2)/2=4) = (1; 0; 4).
Теперь находим симметричные точки как вершины треугольника АВС.
А = 2О - К = (8; -4; 9).
В = 2Р - M = (-1; 2; 3).
C = 2T - N = (-2; 0; 1).