Задача про треугольник и окружность
Как всегда, решу обобщённым и задача принимает следующий вид:
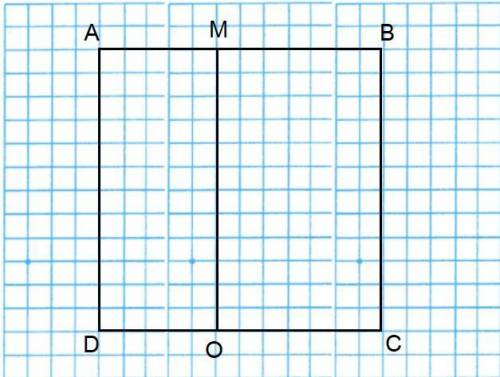
Периметр ΔАВС равен p. Проведена окружность, касающаяся стороны АВ и продолжения сторон АС и ВС. К этой окружности проведена касательная, параллельная прямой АВ, и пересекающая продолжения сторон АС и ВС в точках М и N. Найдите длину АВ, если MN равен а.
По свойству отрезков касательных, проведённых из одной точки к окружности: ME = MT, EN = NP, TA = AS, PB = BS, CP = CT
P (mnc) = MN + CN + CM = ME + EN + NP + PB + BC + MT + TA + AC = 2ME + 2EN + (BS + AS + BC + AC) = 2(ME + EN) + (AB + BC + AC) = 2MN + P (abc)
Значит, P (mnc) = 2MN + P (abc) = 2a + p
MN || AB ⇒ ΔMNC подобен ΔАВС по двум углам, из подобия следует соотношение: P (abc) / P (mnc) = AB/MN
AB = ( P abc / P mnc ) • MN
AB = a•p/(2a + p) = 12•3/(2•3 + 12) = 36/18 = 2
ответ: 2
ответ: S ☐ABCD = 400 см².
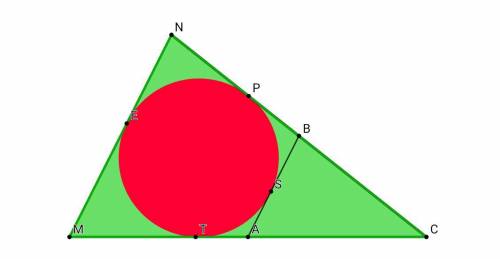
Объяснение: Обозначим квадрат буквами ABCD.
Пусть прямоугольник, периметр которого равен 50 см - DAMO, а прямоугольник, периметр которого равен 70 см - OMBC.
P ▯OMBC = (BC + CO) * 2 = 70 см.
(BC и CO - смежные стороны прямоугольника).
⇒ BC + CO = P/2 ⇒ BC + CO = 70/2 = 35 см.
P ▯DAMO = (AD + DO) * 2 = 50 см.
(AD и DO- смежные стороны прямоугольника).
⇒ AD + DO = P/2 ⇒ AD + DO = 50/2 = 25 см.
AD, DC и CB - стороны данного квадрата.
⇒ AD + DC + CB = 35 + 25 = 60 см.
Т.к. стороны квадрата равны ⇒ AD = DC = CB = 60/3 = 20 см.
⇒ AB = CB = DC = AD = 20 см (т.к. все стороны в квадрате равны).
S ☐ABCD = a² (a - сторона квадрата) ⇒ S ☐ABCD = 20² = 400 см².