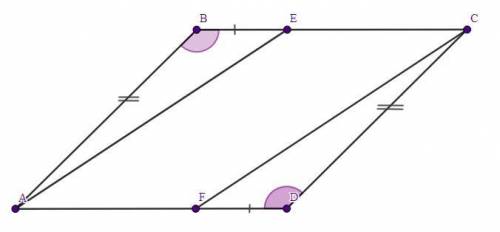
Четырёхугольник ABCD - параллелограмм.
ВЕ = DF (Е ⊂ ВС, F ⊂ AD).
Доказать :Четырёхугольник AECF - параллелограмм.
Доказательство :В параллелограмме противоположные углы и противоположные стороны равны между собой (свойство параллелограмма).Отсюда следует, что ∠В = ∠D, АВ = CD.
Рассмотрим ΔАВЕ и ΔCDF.
ВЕ = DF (по условию)
∠В = ∠D, АВ = CD (по выше сказанному) ⇒ ΔАВЕ = ΔCDF по двум сторонам и углу между ними (первый признак равенства треугольников).
Из равенства треугольников следует и равенство сторон АЕ и CF.
AD = BC (по свойству параллелограмма), но в своё очередь AD = BE + EC ; BC = DF + AF. Учитывая равенство из условия получаем, что ЕС = AF.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм (свойство параллелограмма).АЕ = CF ; ЕС = AF (по выше сказанному) ⇒ четырёхугольник AECF - параллелограмм.
ответ :Что требовалось доказать.
Вычислим величины получившихся дуг. Обозначим их 3х, 5х, 7х и 9х. Сумма их 360 градусов. 3х+5х+7х+9х=360
х=15. Дуги будут 15*3=45, 15*5=75, 15*7=105, 15*9=135.
Углы четырехугольника - вписанные в окружность. Один из них опирается на дугу в 75+105=180. Он будет 90 градусов. Сумма его и противоположного угла 180 градусов. Второй из них 180-90=90 градусов.
Следующий опирается на дугу в 135+105=240 градусов. Его градусная мера 240/2 = 120 градусов. А ему противоположный 180-120=60 градусов.