• Тангенс - это отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике
• Очевидно, что ΔAOB - не является прямоугольным, поэтому проведём из точки O высоту OH на сторону AB треугольника AOB
Тогда тангенс будет равен сумме тангенсов углов BOH и AOH.
• Найдём тангенс угла BOH в прямоугольном ΔBOH:
tg ∠BOH = BH/HO = 3/3 = 1
• Найдём тангенс угла AOH в прямоугольном ΔAOH:
tg ∠AOH = AH/HO = 5/3
• Суммируем значения этих двух тангенсов:
tg ∠AOB = tg ∠BOH + tg ∠AOH = 1 + 5/3 = 8/3 ≈ 2,67
ответ: tg ∠AOB = 8/3
Sin(∠A1AH1) = √6/3. Угол ≈ 54,7°
Объяснение:
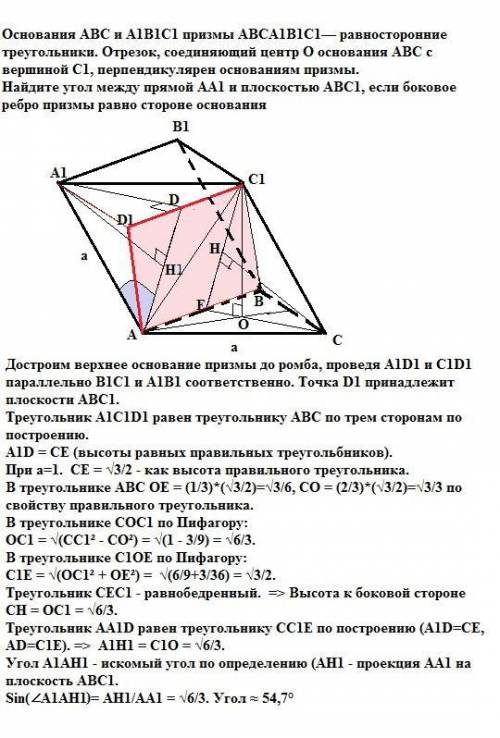
Достроим верхнее основание призмы до ромба, проведя A1D1 и C1D1 параллельно B1C1 и A1B1 соответственно. Точка D1 принадлежит плоскости АВС1.
Треугольник А1С1D1 равен треугольнику АВС по трем сторонам по построению.
A1D = CE (высоты равных правильных треугольников).
При а=1. CE = √3/2 - как высота правильного треугольника.
В треугольнике АВС ОЕ = (1/3)*(√3/2)=√3/6,
СО = (2/3)*(√3/2)=√3/3 по свойству правильного треугольника.
В треугольнике СОС1 по Пифагору:
ОС1 = √(СС1² - СО²) = √(1 - 3/9) = √6/3.
В треугольнике С1ОЕ по Пифагору:
С1Е = √(ОС1² + ОЕ²) = √(6/9+3/36) = √3/2.
Треугольник CEC1 - равнобедренный. => Высота к боковой стороне СН = ОС1 = √6/3.
Треугольник АА1D равен треугольнику СС1Е по построению (A1D=CE, AD=C1E). => A1H1 = C1O = √6/3.
Угол A1АН1 - искомый угол по определению (AH1 - проекция АА1 на плоскость АВС1.
Sin(∠A1AH1) = AH1/AA1 = √6/3. Угол ≈ 54,7°
14.8-7.5=7.3
7.3•2=14.6
14.8-14.6=0.2